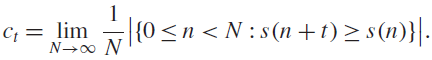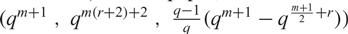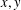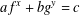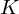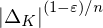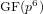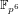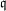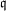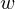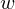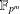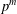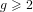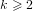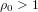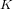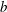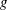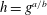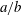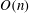Refine search
Actions for selected content:
17 results
A lower bound for Cusick’s conjecture on the digits of n + t
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 139-161
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
NONBINARY DELSARTE–GOETHALS CODES AND FINITE SEMIFIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. S186-S205
- Print publication:
- December 2020
-
- Article
- Export citation
ISOGENIES OF ABELIAN VARIETIES IN CRYPTOGRAPHY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 March 2020, pp. 508-509
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 388-391
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On Zeros of a Polynomial in a Finite Grid
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 310-333
-
- Article
- Export citation
On error distributions in ring-based LWE
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 130-145
-
- Article
-
- You have access
- Export citation
Collecting relations for the number field sieve in
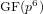 $\text{GF}(p^{6})$
$\text{GF}(p^{6})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 332-350
-
- Article
-
- You have access
- Export citation
Reduced memory meet-in-the-middle attackagainst the NTRU private key
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 43-57
-
- Article
-
- You have access
- Export citation
MORE CONSTRUCTIONS OF APPROXIMATELY MUTUALLY UNBIASED BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 August 2015, pp. 211-222
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Heuristics on pairing-friendly abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 419-443
-
- Article
-
- You have access
- Export citation
A NOTE ON SOME CHARACTER SUMS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 30 April 2015, pp. 32-43
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Constructing abelian surfaces for cryptography via Rosenhain invariants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 157-180
-
- Article
-
- You have access
- Export citation
The discrete logarithm problem for exponents of bounded height
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 148-156
-
- Article
-
- You have access
- Export citation
Finding roots in
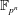 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 203-217
-
- Article
-
- You have access
- Export citation
Complete addition laws on abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 308-316
-
- Article
-
- You have access
- Export citation
Explicit Kummer surface formulas for arbitrary characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 January 2010, pp. 47-64
-
- Article
-
- You have access
- Export citation
Counting irreducible Goppa codes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-306
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation