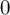 $0$ OVER
$0$ OVER 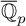 $\overline {\mathbb {Q}}_p$
$\overline {\mathbb {Q}}_p$
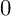 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
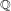 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3