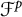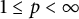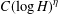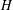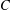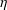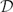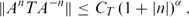Refine search
Actions for selected content:
12 results
On the rate of growth of random analytic functions, with an application to linear dynamics
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1-21
-
- Article
- Export citation
Sparse analytic systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
On unavoidable families of meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 114-123
- Print publication:
- March 2023
-
- Article
- Export citation
ALGEBRAIC VALUES OF CERTAIN ANALYTIC FUNCTIONS DEFINED BY A CANONICAL PRODUCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 415-425
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Entropy of transcendental entire functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 338-348
- Print publication:
- February 2021
-
- Article
- Export citation
GROWTH CONDITIONS FOR OPERATORS WITH SMALLEST SPECTRUM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 665-680
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Integer points of analytic functions in a half-plane
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 619-630
-
- Article
-
- You have access
- Export citation
Even and odd entire functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 19-24
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
About a problem of Hermite and Biehler
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-92
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Growth of functions in cercles de remplissage
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-136
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
About the zeros of some entire functions and their derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-169
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation