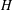 $H$-TYPE GROUPS
$H$-TYPE GROUPS
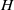 $H$-TYPE GROUPS
$H$-TYPE GROUPS
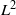 ${L}^{2} $-SINGULAR DICHOTOMY FOR EXCEPTIONAL LIE GROUPS AND ALGEBRAS
${L}^{2} $-SINGULAR DICHOTOMY FOR EXCEPTIONAL LIE GROUPS AND ALGEBRAS
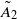 BUILDING
BUILDING