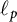 $\ell _p$ spaces
$\ell _p$ spaces
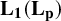 $\mathbf {L_1(L_p)}$ is primary for 1 < p < ∞
$\mathbf {L_1(L_p)}$ is primary for 1 < p < ∞
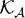 $\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
$\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
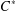 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
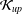 ${\mathcal{K}}_{\mathit{up}}$ -APPROXIMATION PROPERTY AND ITS DUALITY
${\mathcal{K}}_{\mathit{up}}$ -APPROXIMATION PROPERTY AND ITS DUALITY