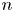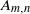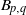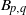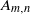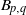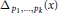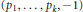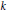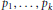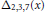Refine search
Actions for selected content:
11 results
Generalized torsion orders and Alexander polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 401-420
- Print publication:
- June 2025
-
- Article
- Export citation
Embedding spheres in knot traces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 20 October 2021, pp. 2242-2279
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALEXANDER POLYNOMIALS OF COMPLEX PROJECTIVE PLANE CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 386-395
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Splitting Numbers of Links
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 03 January 2017, pp. 587-614
-
- Article
- Export citation
Link Floer Homology Categorifies the Conway Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 18 January 2016, pp. 813-836
-
- Article
- Export citation
LENS SPACE SURGERIES ALONG CERTAIN 2-COMPONENT LINKS RELATED WITH PARK’S RATIONAL BLOW DOWN, AND REIDEMEISTER-TURAEV TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 78-126
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Explicit formulae for two-bridge knot polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-166
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
Erratum: The Lehmer Polynomial and Pretzel Links
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 2 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, p. 231
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation
The Lehmer Polynomial and Pretzel Links
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 4 / 01 December 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 440-451
- Print publication:
- 01 December 2001
-
- Article
-
- You have access
- Export citation
ZARISKI PAIRS OF INDEX 19 AND MORDELL–WEIL GROUPS OF K3 SURFACES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 80 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 127-144
- Print publication:
- January 2000
-
- Article
- Export citation
Alexander polynomials of two-bridge knots
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-342
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation