Two-way diffusion equations arising in kinetic problems relating to electron scattering and in Brownian particle dynamics present singularities absent from conventional diffusion equations. Although calculations by Stein & Bernstein, and Fisch & Kruskal have revealed the formation of entry and exit slope discontinuities at the critical points where the velocity changes sign, the analytical structure of these discontinuities remains unclear. Here we fill this gap via a local similarity variable analysis, illustrated through the two-way diffusion equation $y \partial n/\partial x=\partial ^2 n/\partial y^2$ in $-1 \leq y \leq 1$; $0 \leq x \leq L$, with $n(x,\pm 1)=0$ with various entry conditions $n(0,y)_{y\gt 0}$, and the exit condition $n(L,y)_{y\lt 0}=0$. The similarity variable $\eta =y/x^{1/3}$ permits the analytical characterization of the entry discontinuity, except for constants determined by matching with numerical solutions obtained with two numerical schemes: separation of variables following the construction of Beals, or finite-difference discretization of the transient partial differential equation, which converges in time to a solution almost identical to the separation of variables solution. Although the slope discontinuity depends markedly on the initial condition $n(0,y)_{y\gt 0}$, a simple general similarity solution structure emerges empirically, always involving a spontaneous singular contribution $C |y|^{1/2}$ at $x=0,y\lt 0$. Slow convergence of both numerical solutions near $\{x,y\}=\{0,0\}$ is attributed to the poor eigenfunction representation of the ever-present singular solution component $|y|^{1/2}$. The similarity approach applies equally to other two-way diffusion equations when the coefficient of $\partial n/\partial x$ changes sign linearly with $y$. It can also be extended to situations where this coefficient is discontinuous at the critical points.

The spatial organisation of a passive scalar plume originating from a point source in a turbulent boundary layer is studied to understand its meandering characteristics. We focus shortly downstream of the isokinetic injection ($1.5\leqslant x/\delta \leqslant 3$, $\delta$ being the boundary-layer thickness) where the scalar concentration is highly intermittent, the plume rapidly meanders and breaks up into concentrated scalar pockets due to the action of turbulent structures. Two injection locations were considered: the centre of the logarithmic region and the wake region of the boundary layer. Simultaneous quantitative acetone planar laser-induced fluorescence and particle image velocimetry were performed in a wind tunnel, to measure scalar mixture fraction and velocity fields. Single- and multi-point statistics were compared with established works to validate the diagnostic novelties. Additionally, the spatial characteristics of plume intermittency were quantified using ‘blob’ size, shape, orientation and mean concentration. It was observed that straining, breakup and spatial reorganisation were the primary plume-evolution modes in this region, with little small-scale homogenisation. Further, the dominant role of coherent vortex motions in plume meandering and breakup was evident. Their action is found to be the primary mechanism by which the injected scalar is transported away from the wall in high concentrations (‘large meander events’). Strong spatial correlation was observed in both instantaneous and conditional fields between the high-concentration regions and individual vortex heads. This coherent transport was weaker for wake injection, where the plume only interacts with outer vortex motions. A coherent-structure-based mechanism is suggested to explain these transport mechanisms.

Using pore-resolved direct numerical simulation (DNS), we investigate passive scalar transport at a unit Schmidt number in a turbulent flow over a randomly packed bed of spheres. The scalar is introduced at the domain’s free-slip top boundary and absorbed by the bed, which maintains a constant and uniform scalar value on the sphere surfaces. Eight cases are analysed, which are characterised by friction Reynolds numbers of ${\textit{Re}}_\tau \in [150, 500]$ and permeability Reynolds numbers of ${\textit{Re}}_{{\kern-1pt}K} \in [0.4, 2.8]$, while flow depth-to-sphere-diameter ratios vary within $h/D \in \{ 3, 5, 10 \}$ and the roughness Reynolds numbers lie within $k_s^+ \in [20,200]$. For cases with comparable ${\textit{Re}}_\tau$, the permeable wall behaviour enhances scalar absorption, as indicated by increases in the Sherwood number and the scalar roughness function $\Delta c^+$ over ${\textit{Re}}_{{\kern-1pt}K}$. At progressively higher ${\textit{Re}}_{{\kern-1pt}K}$, the scalar absorption diverges increasingly from the momentum absorption, as its distribution peaks deeper below the crests of the sphere pack and spreads over a wider vertical region. The fixed-value scalar boundary condition emphasises certain similarities between the scalar and velocity fields. Near-interface scalar fluctuations are correlated with streamwise velocity fluctuations, and the turbulent Schmidt number remains close to its value in the free-flow region. Compared with zero-flux scalar boundary conditions, prescribing a uniform scalar value on the sphere surfaces reduces spatial heterogeneity within the pore space, thereby limiting both dispersive transport and the form-induced production of temporal scalar fluctuations.

Particle motions under nonlinear gravity waves at the free surface of a two-dimensional incompressible and inviscid fluid are considered. The Euler equations are solved numerically using a high-order spectral method based on a Hamiltonian formulation of the water-wave problem. Extending this approach, a numerical procedure is devised to estimate the fluid velocity at any point in the fluid domain given surface data. The reconstructed velocity field is integrated to obtain particle trajectories for which an analysis is provided, focusing on two questions. The first question is the influence of a wave setup or setdown as is typical in coastal conditions. It is shown that such local changes in the mean water level can lead to qualitatively different pictures of the internal flow dynamics. These changes are also associated with rather strong background currents which dominate the particle transport and, in particular, can be an order of magnitude larger than the well-known Stokes drift. The second question is whether these particle dynamics can be described with a simplified wave model. The Korteweg–de Vries equation is found to provide a good approximation for small- to moderate-amplitude waves on shallow and intermediate water depth. Despite discrepancies in severe cases, it is able to reproduce characteristic features of particle paths for a wave setup or setdown.

We present a mathematical model to investigate heat transfer and mass transport dynamics in the wave-driven free-surface boundary layer of the ocean under the influence of long-crested progressive surface gravity waves. The continuity, momentum and convection–diffusion equations for fluid temperature are solved within a Lagrangian framework. We assume that eddy viscosity and thermometric conductivity are dependent on Lagrangian coordinates, and derive a new form of the second-order Lagrangian mass transport velocity, applicable across the entire finite water depth. We then analyse the convective heat dynamics influenced by the free-surface boundary layer. Rectangular distributions of free-surface temperature (i.e. a Dirichlet boundary condition) are considered, and analytical solutions for thermal boundary layer temperature fields are provided to offer insights into free-surface heat transfer mechanisms affected by ocean waves. Our results suggest the need to improve existing models that neglect the effects of free-surface waves and the free-surface boundary layer on ocean mass transport and heat transfer.

We perform direct numerical simulations of soluble bubbles dissolving in a Taylor–Couette (TC) flow reactor with a radius ratio of $\eta =0.5$ and Reynolds number in the range $0 \leq Re \leq 5000$, which covers the main regimes of this flow configuration, up to fully turbulent Taylor vortex flow. The numerical method is based on a geometric volume-of-fluid framework for incompressible flows coupled with a phase-change solver that ensures mass conservation of the soluble species, whilst boundary conditions on solid walls are enforced through an embedded boundary approach. The numerical framework is validated extensively against single-phase TC flows and competing mass transfer in multicomponent mixtures for an idealised infinite cylinder and for a bubble rising in a quiescent liquid. Our results show that when bubbles in a TC flow are mainly driven by buoyancy, theoretical formulae derived for spherical interfaces on a vertical trajectory still provide the right fundamental relationship between the bubble Reynolds and Sherwood numbers, which reduces to $Sh \propto \sqrt {Pe}$ for large Péclet values. For bubbles mainly transported by TC flows, the dissolution of bubbles depend on the TC Reynolds number and, for the turbulent configurations, we show that the smallest characteristic turbulent scales control mass transfer, in agreement with the small-eddy model of Lamont & Scott (AIChE J., vol. 16, 1970, pp. 513–519). Finally, the interaction between two aligned bubbles is investigated and we show that a significant increase in mass transfer can be obtained when the rotor of the apparatus is operated at larger speeds.

Axisymmetric numerical simulations of the hydrodynamics around rising bubbles are performed in order to investigate the impact of surfactants on the bubble dynamics. Surfactants are assumed to be insoluble. The transport of the adsorbed surfactants is computed along the deforming surface at large surface Péclet number, and Marangoni stresses are taken into account. This simulation model leads to the stagnant-cap regime, with partially immobile interfaces. A parametric study is performed on cases at given Archimedes number, by varying the degree of contamination (Marangoni number) but maintaining a nearly constant Eötvös number. The presence of surfactants affects the rise velocity for oblate bubbles less than for spherical bubbles: the increase of the drag coefficient, due to interface contamination, is mitigated by a lower bubble deformation. When the cap angle $\theta _{cap}$ belongs to the southern hemisphere, the aspect ratio $\chi$ is found to decrease with contamination: the dynamic pressure responsible for the bubble distortion is lowered, related to the decline of kinetic energy. As soon as $\theta _{cap}$ lies in the northern hemisphere, the pressure stress causing distortion becomes independent on $\theta _{cap}: \chi$ no longer evolves with contamination, and already matches the prediction for fully immobile interfaces. Mass transfer of a passive scalar across the contaminated interface is also analysed. Surprisingly, the Sherwood number $Sh$ is found to follow the same law as for spherical shapes (Kentheswaran et al., Intl J. Heat Mass Transfer, vol. 198, 2022, 123325), allowing us to predict the decrease in $Sh$ due to contamination. These results reveal the couplings between interface immobilisation, bubble deformation, rise velocity and interfacial mass transfer.

This paper studies numerically the convection of water vapour in snowpacks using an Eulerian–Eulerian two-phase approach. The convective water vapour transport in snow and its effects on snow density are often invoked to explain observed density profiles, e.g. of thin Arctic snow covers, but this process has never been numerically simulated and analysed in a systematic manner. Here, the impact of convection on the thermal and phase change regimes as a function of different snowpack depths, thermal boundary conditions and Rayleigh numbers is analysed. We find considerable impact of natural convection on the snow density distribution with a layer of significantly lower density at the bottom of the snowpack and a layer of higher density located higher in the snowpack or at the surface. We find that emergent heterogeneity in the snow porosity results in a feedback effect on the spatial organization of convection cells causing their horizontal displacement. Regions where the snowpack is most impacted by phase changes are found to be horizontally extended and vertically thin, ‘pancake’-like layers at the top and bottom of the snowpack. We further demonstrate that among the parameters important for natural convection, the snowpack depth has the strongest influence on the heat and mass transfer. Despite our simplifying assumptions, our study represents a significant improvement over the state of the art and a first step to accurately simulate snowpack dynamics in diverse regions of the cryosphere.

In this paper, we will use optimal mass transport combining with suitable transforms to study the sharp constants and optimizers for a class of the Gagliardo–Nirenberg and Caffarelli–Kohn–Nirenberg inequalities. Moreover, we will investigate these inequalities with and without the monomial weights $x_{1}^{A_{1}} \cdots x_{N}^{A_{N}}$ on ℝN.

The lobe dynamics andmass transport between separation bubble and main flow in flow over airfoil are studied in detail, using Lagrangian coherent structures (LCSs), in order to understand the nature of evolution of the separation bubble. For this problem, the transient flow over NACA0012 airfoil with low Reynolds number is simulated numerically by characteristic based split (CBS) scheme, in combination with dual time stepping. Then, LCSs and lobe dynamics are introduced and developed to investigate themass transport between separation bubble and main flow, from viewpoint of nonlinear dynamics. The results show that stable manifolds and unstable manifolds could be tangled with each other as time evolution, and the lobes are formed periodically to induce mass transport between main flow and separation bubble, with dynamic behaviors. Moreover, the evolution of the separation bubble depends essentially on the mass transport which is induced by lobes, ensuing energy and momentum transfers. As the results, it can be drawn that the dynamics of flow separation could be studied using LCSs and lobe dynamics, and could be controlled feasibly if an appropriate control is applied to the upstream boundary layer with high momentum.

In this paper, weconsider probability measures μ and ν on a d-dimensionalsphere in ${\bf R}^{d+1}, d \geq 1,$ and cost functions of the form $c({\bf x},{\bf y})=l(\frac{|{\bf x}-{\bf y}|^2}{2})$ that generalize those arising in geometric optics where $l(t)=-\log t.$ We prove that if μ and ν vanish on $(d-1)$ -rectifiable sets,if |l'(t)|>0, $\lim_{t\rightarrow 0^+}l(t)=+\infty,$ and $g(t):=t(2-t)(l'(t))^2$ is monotone then thereexists a unique optimal map T o that transports μ onto $\nu,$ whereoptimality is measured against c. Furthermore, $\inf_{{\bf x}}|T_o{\bf x}-{\bf x}|>0.$ Our approach is based on direct variational arguments.In the special case when $l(t)=-\log t,$ existence of optimal maps on thesphere was obtained earlier in [Glimm and Oliker, J. Math. Sci.117 (2003) 4096-4108]and [Wang, Calculus of Variations and PDE's20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that either μ and ν are absolutelycontinuous with respect to the d-dimensional Haussdorff measure, or they have disjoint supports. Another aspect of interestin this work is that it is in contrast with the work in[Gangbo and McCann, Quart. Appl. Math.58 (2000) 705-737] where it is proved that when l(t)=t thenexistence of an optimal map fails when μ and ν are supported by Jordan surfaces.

This article is an edited transcript based on the David Turnbull Lecture given by Ellen D. Williams of the University of Maryland on December 2, 2003, at the Materials Research Society Fall Meeting in Boston.Williams received the award for “groundbreaking research on the atomic-scale science of surfaces and for leadership, writing, teaching, and outreach that convey her deep understanding of and enthusiasm for materials research.” This article focuses on the special properties of small structures that provide much of the exciting potential of nanotechnology.One aspect of small structures—their susceptibility to thermal fluctuations—may create or necessitate new ways of exploiting nanostructures.The advent of scanned probe imaging techniques created new opportunities for observing and understanding such structural fluctuations and the related evolution of nanostructure.Direct observations show that it is relatively easy for large numbers of atoms—the kinds of numbers that are present in nanoscale structures—to pick up and move about on the surface cooperatively with substantial impact on nano-to micron-scale structures.Such labile evolution of structure can be predicted quantitatively by using length-scale bridging techniques of statistical mechanics coupled with scanned probe observations of structural and temporal distributions.The same measurements also provide direct information about the stochastic paths of structural fluctuations that can be used outside of the traditional thermodynamic framework.Future work involves moving beyond the classical thermodynamic picture to assess the impact that the stochastic behavior has on the physical properties of individual nanostructures.

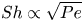
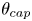
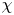
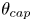
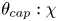
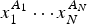
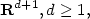
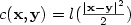
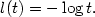
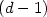
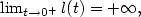
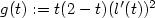
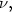
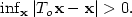
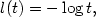
We study the dispersion of a collection of particles carried by an isotropic Brownian flow in Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as t → ∞. In particular, for incompressible flows in two dimensions, we show that the variance of the center of mass grows sublinearly, while dispersion relative to the center of mass grows linearly.