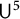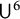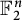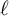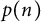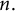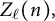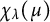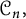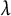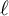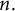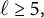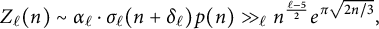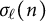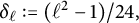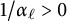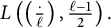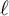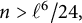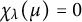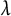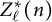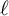Refine search
Actions for selected content:
8 results
Quantitative inverse theorem for Gowers uniformity norms
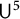 $\mathsf {U}^5$ and
$\mathsf {U}^5$ and 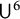 $\mathsf {U}^6$ in
$\mathsf {U}^6$ in 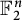 $\mathbb {F}_2^n$
$\mathbb {F}_2^n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1289-1338
- Print publication:
- August 2024
-
- Article
- Export citation
Zeros in the character tables of symmetric groups with an
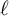 $\ell $-core index
$\ell $-core index
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 June 2022, pp. 467-476
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Involution pipe dreams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 1310-1346
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Constructive Proof of Brauer's Theorem on Induced Characters in the Group Ring

-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 18 December 2013, pp. 31-53
-
- Article
-
- You have access
- Export citation
The group of endotrivial modules for the symmetric and alternating groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 83-95
-
- Article
-
- You have access
- Export citation
Endotrivial modules for the symmetric and alternating groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 45-66
-
- Article
-
- You have access
- Export citation
Partition Algebras are Cellular
-
- Journal:
- Compositio Mathematica / Volume 119 / Issue 1 / October 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 99-109
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
On the eigenvalues of random matrices
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 05 September 2017, pp. 49-62
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation