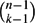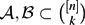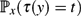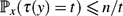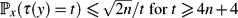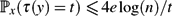Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
On Regularity Lemmas and their Algorithmic Applications
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 28 March 2017, pp. 481-505
-
- Article
- Export citation
Uniform s-Cross-Intersecting Families
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 28 March 2017, pp. 517-524
-
- Article
- Export citation
Minimum Codegree Threshold for C 6 3-Factors in 3-Uniform Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 22 March 2017, pp. 536-559
-
- Article
- Export citation

Groups, Languages and Automata
-
- Published online:
- 16 March 2017
- Print publication:
- 23 February 2017
Preface
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp vii-viii
-
- Chapter
- Export citation
Contents
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp v-vi
-
- Chapter
- Export citation
Surprise Probabilities in Markov Chains
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 603-627
-
- Article
- Export citation
1 - Introduction to Sobolev Spaces
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 1-14
-
- Chapter
- Export citation
6 - Parabolic problems
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 87-118
-
- Chapter
- Export citation
Index
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 207-208
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 201-206
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp i-iv
-
- Chapter
- Export citation
5 - Biharmonic equation
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 59-86
-
- Chapter
- Export citation
7 - Systems in solid mechanics
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 119-130
-
- Chapter
- Export citation
2 - Elliptic scalar problems
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 15-26
-
- Chapter
- Export citation
4 - Interpolation and discretization error
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 47-58
-
- Chapter
- Export citation
9 - Implementation of the finite element method
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 171-200
-
- Chapter
- Export citation
3 - Finite element spaces
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 27-46
-
- Chapter
- Export citation
8 - Systems in fluid mechanics
-
- Book:
- Finite Elements
- Published online:
- 14 December 2017
- Print publication:
- 16 March 2017, pp 131-170
-
- Chapter
- Export citation
A Stability Result for Families with Fixed Diameter
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 506-516
-
- Article
- Export citation