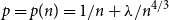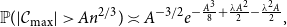Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
6 - Topological Analysis of Point Clouds
-
- Book:
- Computational Topology for Data Analysis
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022, pp 178-206
-
- Chapter
- Export citation
Contents
-
- Book:
- Computational Topology for Data Analysis
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022, pp v-x
-
- Chapter
- Export citation
Index
-
- Book:
- Computational Topology for Data Analysis
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022, pp 429-434
-
- Chapter
- Export citation
13 - Topological Persistence and Machine Learning
-
- Book:
- Computational Topology for Data Analysis
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022, pp 389-410
-
- Chapter
- Export citation
5 - Generators and Optimality
-
- Book:
- Computational Topology for Data Analysis
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022, pp 148-177
-
- Chapter
- Export citation
References
-
- Book:
- Computational Topology for Data Analysis
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022, pp 411-428
-
- Chapter
- Export citation

Pop-Up Geometry
- The Mathematics Behind Pop-Up Cards
-
- Published online:
- 03 March 2022
- Print publication:
- 24 March 2022
Refined universality for critical KCM: lower bounds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 879-906
-
- Article
- Export citation

Computational Topology for Data Analysis
-
- Published online:
- 18 February 2022
- Print publication:
- 10 March 2022
Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 840-869
-
- Article
- Export citation
Short proofs for long induced paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 870-878
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Theoretical Computer Science for the Working Category Theorist
-
- Published online:
- 25 January 2022
- Print publication:
- 03 March 2022
-
- Element
- Export citation
Removal lemmas and approximate homomorphisms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 721-736
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
12 - Parameter table
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp 399-424
-
- Chapter
- Export citation
Preface
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp xv-xviii
-
- Chapter
- Export citation
4 - Buildings
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp 114-138
-
- Chapter
- Export citation
7 - Cyclotomic constructions
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp 174-196
-
- Chapter
- Export citation
Parameter Index
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp 451-452
-
- Chapter
- Export citation
8 - Combinatorial constructions
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp 197-248
-
- Chapter
- Export citation
Contents
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp v-xiv
-
- Chapter
- Export citation