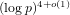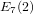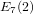Refine search
Actions for selected content:
48276 results in Computer Science
Chapter 23 - Unary Symmetry
- from Part 2 - Unary Pure Inductive Logic
-
- Book:
- Pure Inductive Logic
- Published online:
- 05 May 2015
- Print publication:
- 02 April 2015, pp 171-178
-
- Chapter
- Export citation
Chapter 12 - Asymptotic Conditional Probabilities
- from Part 2 - Unary Pure Inductive Logic
-
- Book:
- Pure Inductive Logic
- Published online:
- 05 May 2015
- Print publication:
- 02 April 2015, pp 73-80
-
- Chapter
- Export citation
Part 2 - Unary Pure Inductive Logic
-
- Book:
- Pure Inductive Logic
- Published online:
- 05 May 2015
- Print publication:
- 02 April 2015, pp 47-48
-
- Chapter
- Export citation
Part 3 - Polyadic Pure Inductive Logic
-
- Book:
- Pure Inductive Logic
- Published online:
- 05 May 2015
- Print publication:
- 02 April 2015, pp 179-180
-
- Chapter
- Export citation
Chapter 31 - Representation Theorems for Sx
- from Part 3 - Polyadic Pure Inductive Logic
-
- Book:
- Pure Inductive Logic
- Published online:
- 05 May 2015
- Print publication:
- 02 April 2015, pp 223-238
-
- Chapter
- Export citation
Coleman integration for even-degree models of hyperelliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 258-265
-
- Article
-
- You have access
- Export citation
On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 308-322
-
- Article
-
- You have access
- Export citation
Champ: a Cherednik algebra Magma package
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 266-307
-
- Article
-
- You have access
- Export citation
The maximal subgroups of
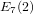 $E_{7}(2)$
$E_{7}(2)$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 323-371
-
- Article
-
- You have access
- Export citation
Piecewise Legendre spectral-collocation method for Volterra integro-differential equations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 231-249
-
- Article
-
- You have access
- Export citation
Computing overconvergent forms for small primes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 250-257
-
- Article
-
- You have access
- Export citation
A NEGLECTED RESOLUTION OF RUSSELL’S PARADOX OF PROPOSITIONS
-
- Journal:
- The Review of Symbolic Logic / Volume 8 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 31 March 2015, pp. 328-344
- Print publication:
- June 2015
-
- Article
- Export citation
ANALYSIS OF MARKOV-MODULATED INFINITE-SERVER QUEUES IN THE CENTRAL-LIMIT REGIME
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 29 / Issue 3 / July 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 433-459
-
- Article
- Export citation
EVIDENTIAL SUPPORT, TRANSITIVITY, AND SCREENING-OFF
-
- Journal:
- The Review of Symbolic Logic / Volume 8 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 785-806
- Print publication:
- December 2015
-
- Article
- Export citation
PES volume 29 issue 2 Cover and Back matter
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 29 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Distance closures on complex networks
-
- Journal:
- Network Science / Volume 3 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 227-268
-
- Article
- Export citation
ON A GENERALIZATION OF THE STATIONARY EXCESS OPERATOR
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 29 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 219-232
-
- Article
- Export citation
PES volume 29 issue 2 Cover and Front matter
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 29 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
EXACT DISTRIBUTION OF INTERMITTENTLY CHANGING POSITIVE AND NEGATIVE COMPOUND POISSON PROCESS DRIVEN BY AN ALTERNATING RENEWAL PROCESS AND RELATED FUNCTIONS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 29 / Issue 3 / July 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 385-397
-
- Article
- Export citation
6 - Classification of Data
-
- Book:
- Large Sample Covariance Matrices and High-Dimensional Data Analysis
- Published online:
- 05 April 2015
- Print publication:
- 26 March 2015, pp 75-104
-
- Chapter
- Export citation