Refine search
Actions for selected content:
25847 results in Abstract analysis
A Sárközy Theorem for Finite Fields
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 643-651
-
- Article
- Export citation
Ramsey Games Against a One-Armed Bandit
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 515-545
-
- Article
- Export citation
Canonical Vertex Partitions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 671-704
-
- Article
- Export citation
Open Problems in Partition Regularity
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 571-583
-
- Article
- Export citation
A Note on Explicit Ramsey Graphs and Modular Sieves
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 565-569
-
- Article
- Export citation
Markov Processes and Ramsey Theory for Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 547-563
-
- Article
- Export citation
On the Erdős–Simonovits–Sós Conjecture about the Anti-Ramsey Number of a Cycle
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 585-598
-
- Article
- Export citation
On the Canonical Version of a Theorem in Ramsey Theory
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 513-514
-
- Article
- Export citation
Mixed Ramsey Numbers Revisited
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 653-660
-
- Article
- Export citation
An Application of Hindman's Theorem to a Problem on Communication Complexity
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 661-670
-
- Article
- Export citation
On Ramsey Numbers of Sparse Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 627-641
-
- Article
- Export citation
A Partition Theorem for Scattered Order Types
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 621-626
-
- Article
- Export citation
Local Anti-Ramsey Numbers of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 12 / Issue 5-6 / November 2003
- Published online by Cambridge University Press:
- 03 December 2003, pp. 495-511
-
- Article
- Export citation
Index to volume 50
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, p. 221
- Print publication:
- December 2003
-
- Article
- Export citation
The equation ω(n) = ω(n + 1)
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- December 2003
-
- Article
- Export citation
Book Reviews - A. K. Agarwal, B. C. Berndt, C. F. Krattenthaler, G. L. Mullen, K. Ramachandra and M. Waldschmidt (EDITORS). Number Theory and Discrete Mathematics. Birkhäuser (Basel), 2002; 314 pp. ISBN 3 7643 6720 2 (hardback), £59 (approx.). - J.-P. Allouche and J. Shallit. Automatic Sequences, Theory, Applications, Generalizations. Cambridge University Press, 2003; 571 pp. ISBN 0 521 82332 3 (hardback), £37.50. - H. Anton and R. C. Busby. Contemporary Linear Algebra. Wiley and Sons (New York), 2003; 594 pp. ISBN 0 471 16362 7 (hardback), £31.95. - G. Cohen. A Course in Modern Analysis and its Applications. Australian Mathematical Society Lecture Series 17, Cambridge University Press, 2003; 333 pp. ISBN 0 521 81996 2 (hardback), £60; 0 521 52627 2 (paperback), £24.95. - G. Davidoff, P. Sarnak and A. Valette. Elementary Number Theory. Group Theory and Ramanujan Graphs. London Mathematical Society Student Texts 55, Cambridge University Press, 2003; 144 pp. ISBN 0 521 82426 5 (hardback), £47.50; 0 521 53143 8 (paperback). - K. Falconer. Fractal Geometry (2nd edition). John Wiley and Sons (Chichester), 2003; 337 pp. ISBN 0 470 84861 8 (hardback). £42 (approx.); 0 470 84862 6 (paperback). - T. Forster. Logic, Induction and Sets. London Mathematical Society Student Texts 56, Cambridge University Press, 2003; 234 pp. ISBN 0 521 82621 7 (hardback), £50; 0 521 53361 9 (paperback), £18.95. - W. T. Gowers. Mathematics: A Very Short Introduction. Oxford University Press, 2002; 143 pp. ISBN 0 19 285361 9 (paperback), £6.99. - C. W. Henson, J. Iovino, A. S. Kechris and E. Odell. Analysis and Logic. London Mathematical Society Lecture Note Series 262. Cambridge University Press, 2002; 267 pp. ISBN 0 521 64861 0 (paperback), £29.95. - G. J. O. Jameson. The Prime Number Theorem. London Mathematical Society Student Texts 53, Cambridge University Press, 2003; 252 pp. ISBN 0 521 81411 1 (hardback), £50; 0 521 89110 8 (paperback), £18.95. - F. E. A. Johnson. Stable Modules and the D(2)-Problem. London Mathematical Society Lecture Note Series 301, Cambridge University Press, 2003; 267 pp. ISBN 0 521 53749 5 (paperback), £29.95. - J. Lewin. An Interactive Introduction to Mathematical Analysis. Cambridge University Press, 2003; 492 pp. ISBN 0 521 81589 4 (hardback); 0 521 01718 (paperback). £27.95. - S. Mukai. An Introduction to Invariants and Moduli. Cambridge Studies in Advanced Mathematics 81, Cambridge University Press, 2003; 503 pp. ISBN 521 80906 1 (hardback), £65. - R. J. Nowakowski (EDITOR). Games of No Chance, Combinatorial Games at MSRI, 1994. Cambridge University Press, 1996; 537 pp. ISBN 0 521 57411 0 (hardback), £40; 0 521 64652 9 (paperback), £19.95. - R. J. Nowakowski (EDITOR). More Games of No Chance. Cambridge University Press, 2002; 535 pp. ISBN 0 521 80832 4 (hardback), £40. - C. Pritchard (EDITOR). The Changing Shape of Geometry. Celebrating a Century of Geometry and Geometry Teaching. Mathematical Association of America, Cambridge University Press, 2003; 541 pp. ISBN 0 521 82451 6 (hardback), £65; 0 521 53162 4 (paperback), £24.95. - T. Sheil-Small. Complex Polynomials. Cambridge Studies in Advanced Mathematics 75, Cambridge University Press, 2002; 428 pp. ISBN 0 521 40068 6 (hardback), £65. - J. A. Stedall. The Greate Invention of Algebra: Thomas Harriot's “Treatise on Equations”. Oxford University Press, 2003; 322 pp. ISBN 0 19 8526024 (hardback), £65. - J. Stopple. A Primer of Analvtk Number Theory. Cambridge University Press, 2003; 383 pp. ISBN 0 521 81309 3 (hardback), £65; 0 521 01253 8 (paperback), £22.95. - H. A. van der Vorst. Iterative Krylov Methods for Large Linear Systems. Cambridge Monographs on Applied and Computational Mathematics 13, Cambridge University Press, 2003; 221 pp. ISBN 0 521 81828 1 (hardback), £37.50. - C. D. Wensley (EDITOR). Surveys in Combinatorics2003. London Mathematical Society Lecture Note Series 307, Cambridge University Press, 2003: 370 pp. ISBN 0 521 54012 7 (paperback), £34.95.
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-219
- Print publication:
- December 2003
-
- Article
- Export citation
Rank-one convexity implies quasi-convexity on certain hypersurfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 6 / December 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1263-1272
- Print publication:
- December 2003
-
- Article
- Export citation
Corrigendum
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 6 / December 2003
- Published online by Cambridge University Press:
- 12 July 2007, p. 1421
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Quadratic polynomials, factorization in integral domains and Schreier domains from pullbacks
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-112
- Print publication:
- December 2003
-
- Article
- Export citation
On GLn(ℝ)-invariant classes of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-61
- Print publication:
- December 2003
-
- Article
- Export citation
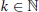 and any positive density subset
and any positive density subset 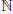 , there exist elements
, there exist elements 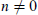 such that
such that 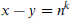 . A version of this result for finite fields is derived from a recent theorem of P. Larick, a short proof of which is also given.
. A version of this result for finite fields is derived from a recent theorem of P. Larick, a short proof of which is also given.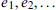 of a complete graph on
of a complete graph on 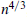 , the proof of the upper bound suggests the following relaxation: instead of colouring online, the random graph is generated in only two rounds, and the Player colours the edges of the first round before the edges of the second round are thrown in. Given the size of the first round, how many edges can there be in the second round for the Player to be likely to win? In the extreme case, when the first round consists of a random graph with
, the proof of the upper bound suggests the following relaxation: instead of colouring online, the random graph is generated in only two rounds, and the Player colours the edges of the first round before the edges of the second round are thrown in. Given the size of the first round, how many edges can there be in the second round for the Player to be likely to win? In the extreme case, when the first round consists of a random graph with 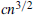 edges, where
edges, where 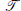 be a set of finite complete relational structures of signature σ, and let
be a set of finite complete relational structures of signature σ, and let 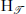 be the countable homogeneous relational structure of signature σ which does not embed any of the structures in
be the countable homogeneous relational structure of signature σ which does not embed any of the structures in 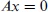 . Many of the classical theorems of Ramsey Theory may naturally be interpreted as assertions that particular matrices are partition regular.
. Many of the classical theorems of Ramsey Theory may naturally be interpreted as assertions that particular matrices are partition regular.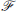 of graphs, let
of graphs, let 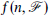 denote the maximum number of colours in an edge-colouring of
denote the maximum number of colours in an edge-colouring of 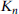 such that no subgraph of
such that no subgraph of 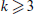 that
that 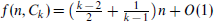 . This has been proved for
. This has been proved for 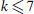 . For general
. For general 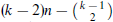 to
to 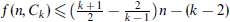 . For even
. For even 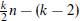 . We also prove that
. We also prove that 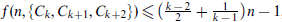 , which is sharp.
, which is sharp.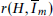 is the smallest integer
is the smallest integer  , (ii) with
, (ii) with 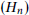 a sequence of dense graphs, in particular for the sequence
a sequence of dense graphs, in particular for the sequence 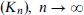 . Open problems are mentioned throughout the paper.
. Open problems are mentioned throughout the paper.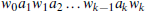 , for fixed letters
, for fixed letters  . Using the well-known theorem of Hindman (a Ramsey-type result about finite subsets of natural numbers), we prove that for
. Using the well-known theorem of Hindman (a Ramsey-type result about finite subsets of natural numbers), we prove that for 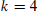 and 5 the communication complexity of the problem increases with the length of the word
and 5 the communication complexity of the problem increases with the length of the word 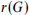 , of a graph
, of a graph 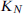 on
on 
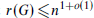 for each such
for each such  , sufficiently large
, sufficiently large 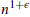 , either
, either 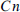 such that neither
such that neither 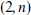 -common graph.
-common graph.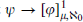 holds.
holds.