We analyse the non-commutative space underlying the quantum group $\textrm{SU}_q(2)$ from the spectral point of view, which is the basis of non-commutative geometry, and show how the general theory developed in our joint work with Moscovici applies to the specific spectral triple defined by Chakraborty and Pal. This provides the pseudo-differential calculus, the Wodzciki-type residue, and the local cyclic co-cycle giving the index formula. The co-chain whose co-boundary is the difference between the original Chern character and the local one is given by the remainders in the rational approximation of the logarithmic derivative of the Dedekind eta function. This specific example allows us to illustrate the general notion of locality in non-commutative geometry. The formulae computing the residue are ‘local’. Locality by stripping all the expressions from irrelevant details makes them computable. The key feature of this spectral triple is its equivariance, i.e. the $\textrm{SU}_q(2)$-symmetry. We shall explain how this naturally leads to the general concept of invariant cyclic cohomology in the framework of quantum group symmetries.

AMS 2000 Mathematics subject classification: Primary 81R50; 19K33; 46L; 58B34

The relative rank $\rank(S:A)$ of a subset $A$ of a semigroup $S$ is the minimum cardinality of a set $B$ such that $\langle A\cup B\rangle=S$. It follows from a result of Sierpiński that, if $X$ is infinite, the relative rank of a subset of the full transformation semigroup $\mathcal{T}_{X}$ is either uncountable or at most $2$. A similar result holds for the semigroup $\mathcal{B}_{X}$ of binary relations on $X$.

A subset $S$ of $\mathcal{T}_{\mathbb{N}}$ is dominated (by $U$) if there exists a countable subset $U$ of $\mathcal{T}_{\mathbb{N}}$ with the property that for each $\sigma$ in $S$ there exists $\mu$ in $U$ such that $i\sigma\le i\mu$ for all $i$ in $\mathbb{N}$. It is shown that every dominated subset of $\mathcal{T}_{\mathbb{N}}$ is of uncountable relative rank. As a consequence, the monoid of all contractions in $\mathcal{T}_{\mathbb{N}}$ (mappings $\alpha$ with the property that $|i\alpha-j\alpha|\le|i-j|$ for all $i$ and $j$) is of uncountable relative rank.

It is shown (among other results) that $\rank(\mathcal{B}_{X}:\mathcal{T}_{X})=1$ and that $\rank(\mathcal{B}_{X}:\mathcal{I}_{X})=1$ (where $\mathcal{I}_{X}$ is the symmetric inverse semigroup on $X$). By contrast, if $\mathcal{S}_{X}$ is the symmetric group, $\rank(\mathcal{B}_{X}:\mathcal{S}_{X})=2$.

AMS 2000 Mathematics subject classification: Primary 20M20

In this paper spectral properties of non-selfadjoint Jacobi operators $J$ which are compact perturbations of the operator $J_0=S+\rho S^*$, where $\rho\in(0,1)$ and $S$ is the unilateral shift operator in $\ell^2$, are studied. In the case where $J-J_0$ is in the trace class, Friedrichs’s ideas are used to prove similarity of $J$ to the rank one perturbation $T$ of $J_0$, i.e. $T=J_0+(\cdot,p)e_1$. Moreover, it is shown that the perturbation is of ‘smooth type’, i.e. $p\in\ell^2$ and

$$ \varlimsup_{n\rightarrow\infty}|p(n)|^{1/n}\le\rho^{1/2}. $$

When $J-J_0$ is not in the trace class, the Friedrichs method does not work and the transfer matrix approach is used. Finally, the point spectrum of a special class of Jacobi matrices (introduced by Atzmon and Sodin) is investigated.

AMS 2000 Mathematics subject classification: Primary 47B36. Secondary 47B37

We provide uniqueness results for holomorphic functions in the Nevanlinna class which bridge those previously obtained by Hayman and by Lyubarskii and Seip. In particular, we propose certain classes of hyperbolically separated sequences in the disc, in terms of the rate of non-tangential accumulation to the boundary (the outer limits of this spectrum of classes being, respectively, the sequences with a non-tangential cluster set of positive measure, and the sequences satisfying the Blaschke condition). For each of those classes, we give a critical condition of radial decrease on the modulus which will force a Nevanlinna class function to vanish identically.

AMS 2000 Mathematics subject classification: Primary 30D50; 30D55

Let $X$ be a surface in $\mathbb{C}^n$ or $\mathbb{P}^n$ and let $C_{X}(X\times X)$ be the normal cone to $X$ in $X\times X$ (diagonally embedded). For a point $x\in X$, denote by $g(x):=e_x(C_X(X\times X))$ the multiplicity of $C_X(X\times X)$ at $x$. It is a former result of the authors that $g(x)$ is the degree at $x$ of the Stückrad–Vogel cycle $v(X,X)=\sum_C j(X,X;C)[C]$ of the self-intersection of $X$, that is, $g(x)=\sum_Cj(X,X;C)e_x(C)$. We prove that the stratification of $X$ by the multiplicity $g(x)$ is a Whitney stratification, the canonical one if $n=3$. The corresponding result for hypersurfaces in $\mathbb{A}^n$ or $\mathbb{P}^n$, diagonally embedded in a multiple product with itself, was conjectured by van Gastel. This is also discussed, but remains open.

AMS 2000 Mathematics subject classification: Primary 32S15. Secondary 13H15;14C17

In this paper the authors establish the $L^p$ boundedness for several classes of Marcinkiewicz integral operators with kernels satisfying a condition introduced by Grafakos and Stefanov in Indiana Univ. Math. J.47 (1998), 455–469.

AMS 2000 Mathematics subject classification: Primary 42B25; 42B99

In this paper we study the existence of multiple positive solutions and the bifurcation problem for the following equation:

$$ -\Delta u+u=\biggl(\int_{\mathbb{R}^3}\frac{|u(y)|^2}{|x-y|}\,\mathrm{d}y\biggr)u+\mu f(x),\quad x\in\mathbb{R}^3, $$

where $f(x)\in H^{-1}(\mathbb{R}^3)$, $f(x)\geq0$, $f(x)\not\equiv0$. We show that there are positive constants $\mu^{*}$ and $\mu^{**}$ such that the above equation possesses at least two positive solutions for $\mu\in(0,\mu^{*})$, and no positive solution for $\mu>\mu^{**}$. Furthermore, we prove that $\mu=\mu^{*}$ is a bifurcation point for the equation under study.

AMS 2000 Mathematics subject classification: Primary 35J60; 35J70

In this paper, we use the theorem of Burchnall and Shaundy to give the capacity of the spectrum $\sigma(A)$ of a periodic tridiagonal and symmetric matrix. A special family of Chebyshev polynomials of $\sigma(A)$ is also given. In addition, the inverse problem is considered: given a finite union $E$ of closed intervals, we study the conditions for a Jacobi matrix $A$ to exist satisfying $\sigma(A)=E$. We relate this question to Carathéodory theorems on conformal mappings.

AMS 2000 Mathematics subject classification: Primary 31B15; 30C20; 39A70

We develop a method of reducing the size of quantum minors in the algebra of quantum matrices $\mathcal{O}_q(M_n)$. We use the method to show that the quantum determinantal factor rings of $\mathcal{O}_q(M_n)c$ are maximal orders, for $q$ an element of $\mathbb{C}$ transcendental over $\mathbb{Q}$.

AMS 2000 Mathematics subject classification: Primary 16P40; 16W35; 20G42

We consider symplectic difference systems, which contain as special cases linear Hamiltonian difference systems and Sturm–Liouville difference equations of any even order. An associated discrete quadratic functional is important in discrete variational analysis, and while its positive definiteness has been characterized and is well understood, a characterization of its positive semidefiniteness remained an open problem. In this paper we present the solution to this problem and offer necessary and sufficient conditions for such discrete quadratic functionals to be non-negative definite.

AMS 2000 Mathematics subject classification: Primary 39A12; 39A13. Secondary 34B24; 49K99

The Equation (1) $(r(x)y')'=q(x)y(x)$ is regarded as a perturbation of (2) $(r(x)z'(x))'=q_1(x)z(x)$. The functions $r(x)$, $q_1(x)$ are assumed to be continuous real valued, $r(x)>0$, $q_1(x)\ge0$, whereas $q(x)$ is continuous complex valued. A problem of Hartman and Wintner regarding the asymptotic integration of (1) for large $x$ by means of solutions of (2) is studied. Sufficiency conditions for solvability of this problem expressed by means of coefficients $r(x)$, $q(x)$, $q_1(x)$ of Equations (1) and (2) are obtained.

AMS 2000 Mathematics subject classification: Primary 34E20

A symplectic connection on a symplectic manifold, unlike the Levi-Civita connection on a Riemannian manifold, is not unique. However, some spaces admit a canonical connection (symmetric symplectic spaces, Kähler manifolds, etc.); besides, some ‘preferred’ symplectic connections can be defined in some situations. These facts motivate a study of the symplectic connections, inducing a parallel Ricci tensor. This paper gives the possible forms of the Ricci curvature on such manifolds and gives a decomposition theorem (linked with the holonomy decomposition) for them.

AMS 2000 Mathematics subject classification: Primary 53B05; 53B30; 53B35; 53C25; 53C55

It is well known that every non-reflexive $M$-ideal is weakly compactly generated (in short, WCG). We present a family of Banach spaces $\{V_{s}:0 \lt s \lt 1\}$ which are not WCG and such that every $V_{s}$ satisfies the inequality

$$ \|\f\|\geq\|\pi\f\|+s\|\f-\pi\f\|\quad\forall\f\in V_{s}^{\ast\ast\ast}, $$

where $\pi$ is the canonical projection from $V_{s}^{\ast\ast\ast}$ onto $V_{s}^{\ast}$. In particular, no $V_{s}$ can be renormed to be an $M$-ideal.

AMS 2000 Mathematics subject classification: Primary 46B20

Given an embedded hypersurface $M$ in $\mathbb{R}^4$ we consider families of projections $H$ of $M$ to lines and families of projections $P$ of $M$ to 3-spaces. We characterize generically the singularities of these projections. We also show that there is a duality relation between some strata of the bifurcation sets of $H$ and $P$, and deduce geometric properties about these sets.

AMS 2000 Mathematics subject classification: Primary 58K05. Secondary 58K40

The notion of $B$-convexity for operator spaces, which a priori depends on a set of parameters indexed by $\sSi$, is defined. Some of the classical characterizations of this geometric notion for Banach spaces are studied in this new context. For instance, an operator space is $B_{\sSi}$-convex if and only if it has $\sSi$-subtype. The class of uniformly non-$\mathcal{L}^1(\sSi)$ operator spaces, which is also the class of $B_{\sSi}$-convex operator spaces, is introduced. Moreover, an operator space having non-trivial $\sSi$-type is $B_{\sSi}$-convex. However, the converse is false. The row and column operator spaces are nice counterexamples of this fact, since both are Hilbertian. In particular, this result shows that a version of the Maurey–Pisier Theorem does not hold in our context. Some other examples of Hilbertian operator spaces will be considered. In the last part of this paper, the independence of $B_{\sSi}$-convexity with respect to $\sSi$ is studied. This provides some interesting problems, which will be posed.

AMS 2000 Mathematics subject classification: Primary 46L07. Secondary 42C15

By means of monotone functionals and positive linear functionals defined on suitable matrix spaces as well as new generalized Riccati transformations, oscillation criteria for self-adjoint linear Hamiltonian matrix systems are obtained. Our results are generalizations and improvements of many existing results.

AMS 2000 Mathematics subject classification: Primary 34A30; 34C10

The relationships between various notions of completeness of eigenvectors and root vectors of the eigenvalue problem $Af=\lambda Bf$ are investigated. Here $A$ and $B$ are self-adjoint operators in Hilbert space with $B$ bounded and positive semidefinite, and with $A$ having compact resolvent.

AMS 2000 Mathematics subject classification: Primary 47A75. Secondary 34B24; 35P10

The van der Waerden theorem in Ramsey theory states that, for every k and t and sufficiently large N, every k-colouring of [N] contains a monochromatic arithmetic progression of length t. Motivated by this result, Radoičić conjectured that every equinumerous 3-colouring of [3n] contains a 3-term rainbow arithmetic progression, i.e., an arithmetic progression whose terms are coloured with distinct colours. In this paper, we prove that every 3-colouring of the set of natural numbers for which each colour class has density more than 1/6, contains a 3-term rainbow arithmetic progression. We also prove similar results for colourings of . 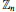Finally, we give a general perspective on other anti-Ramsey-type problems that can be considered.

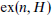For a graph H and an integer n, the Turán number is the maximum possible number of edges in a simple graph on n vertices that contains no copy of H. H is r-degenerate if every one of its subgraphs contains a vertex of degree at most r. We prove that, for any fixed bipartite graph H in which all degrees in one colour class are at most r, . This is tight for all values of r and can also be derived from an earlier result of Füredi. We also show that there is an absolute positive constant c such that, for every fixed bipartite r-degenerate graph H, This is motivated by a conjecture of Erdős that asserts that, for every such H,

For two graphs G and H, the Ramsey number is the minimum number 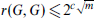n such that, in any colouring of the edges of the complete graph on n vertices by red and blue, there is either a red copy of G or a blue copy of H. Erdős conjectured that there is an absolute constant c such that, for any graph G with m edges, . Here we prove this conjecture for bipartite graphs 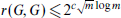G, and prove that for general graphs G with m edges, for some absolute positive constant c.

These results and some related ones are derived from a simple and yet surprisingly powerful lemma, proved, using probabilistic techniques, at the beginning of the paper. This lemma is a refined version of earlier results proved and applied by various researchers including Rödl, Kostochka, Gowers and Sudakov.