Refine search
Actions for selected content:
25814 results in Abstract analysis
A note on groups with non-central norm
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 37-43
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Harmonic maps from noncompact Riemannian manifolds with non-negative Ricci curvature outside a compact set
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1259-1275
- Print publication:
- 1994
-
- Article
- Export citation
Almost factorisable inverse semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-111
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
PRM volume 124 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
GMJ volume 36 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
On the fixpoints of composite entire functions of finite order
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 995-1001
- Print publication:
- 1994
-
- Article
- Export citation
Integral maximum principle and its applications
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 353-362
- Print publication:
- 1994
-
- Article
- Export citation
Localising and seminormal composition operators on L2
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 301-316
- Print publication:
- 1994
-
- Article
- Export citation
On the vanishing viscosity in the Cauchy problem for the equations of a nonhomogeneous incompressible fluid
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-129
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
M-function behaviour for a periodic Dirac system
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 149-159
- Print publication:
- 1994
-
- Article
- Export citation
Blow-up for quasilinear heat equations with critical Fujita's exponents
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 517-525
- Print publication:
- 1994
-
- Article
- Export citation
Poincaré–Bendixson theory for certain reaction–diffusion boundary-value problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 33-69
- Print publication:
- 1994
-
- Article
- Export citation
Conjugacy classes in sylow p-subgroups of GL(n, q), IV†
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 91-96
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Products of nilpotent linear transformations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1135-1150
- Print publication:
- 1994
-
- Article
- Export citation
Elliptic solutions and blow-up in an integrable Hénon–Heiles system
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1151-1164
- Print publication:
- 1994
-
- Article
- Export citation
On the nilpotent ranks of certain semigroups of transformations
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-9
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Homogenisation of two-phase emulsions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1119-1134
- Print publication:
- 1994
-
- Article
- Export citation
Time-dependent solutions of the Navier–Stokes equations for spatially-uniform velocity gradients
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 127-136
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
On the uniqueness of arithmetic structures
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1037-1044
- Print publication:
- 1994
-
- Article
- Export citation

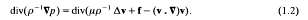
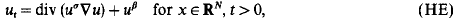
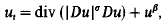
 , the Sylow
, the Sylow