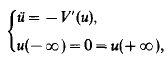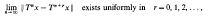Refine search
Actions for selected content:
25814 results in Abstract analysis
The Chen-type of the noncompact cyclides of Dupin
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 71-75
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
28 real bitangents: Dedicated to Ian Porteus
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 729-736
- Print publication:
- 1994
-
- Article
- Export citation
Multiple homoclinic orbits for autonomous, singular potentials
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 785-802
- Print publication:
- 1994
-
- Article
- Export citation
Schottky uniformizations of closed Riemann surfaces with Abelian groups of conformal automorphisms
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 17-32
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Relaxation of quasi-convex integrals of arbitrary order
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 927-946
- Print publication:
- 1994
-
- Article
- Export citation
Invariant algebraic curves and conditions for a centre
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1209-1229
- Print publication:
- 1994
-
- Article
- Export citation
An ergodic theorem for asymptotically nonexpansive mappings
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 23-31
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
Very weak solutions of boundary value problems for the Laplace operator and the Lamé system on polyhedral domains in ℝ3
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 645-672
- Print publication:
- 1994
-
- Article
- Export citation
Cockcroft properties of graphs of 2-complexes
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 363-369
- Print publication:
- 1994
-
- Article
- Export citation
A nonlocal Sturm–Liouville eigenvalue problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 169-188
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 6 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
On an arithemtical inequality
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 81-86
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Nilpotent local automorphisms of an independence algebra
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 423-436
- Print publication:
- 1994
-
- Article
- Export citation
Each univariate complex polynomial has a ‘big’ factor
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 71-76
- Print publication:
- 1994
-
- Article
- Export citation
Closed geodesics in Riemannian manifolds with convex boundary*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1247-1258
- Print publication:
- 1994
-
- Article
- Export citation
Local minimisers of a three-phase partition problem with triple junctions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1059-1073
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 6 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
Finite semilattices whose non-invertible endomorphisms are products of idempotents
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1193-1198
- Print publication:
- 1994
-
- Article
- Export citation
Residual finiteness of free products of combinatorial strict inverse semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 137-147
- Print publication:
- 1994
-
- Article
- Export citation