Refine search
Actions for selected content:
25814 results in Abstract analysis
Decay rates of the solutions of nonlinear dispersive equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1231-1246
- Print publication:
- 1994
-
- Article
- Export citation
A note on locally soluble, normal closures of cyclic subgroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 33-36
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
PRM volume 124 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
Abstract initial boundary value problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 879-908
- Print publication:
- 1994
-
- Article
- Export citation
On the regularity of stochastic difference equations in hyperfinite-dimensional vector spaces and applications to
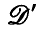 -valued stochastic differential equations
-valued stochastic differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1089-1117
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
Maximal torsional rigidity: some qualitative remarks
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 971-994
- Print publication:
- 1994
-
- Article
- Export citation
A Phragmén–Lindelöf principle for the equation of a surface of constant mean curvature
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 105-119
- Print publication:
- 1994
-
- Article
- Export citation
Stability of the interface in a model of phase separation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1013-1022
- Print publication:
- 1994
-
- Article
- Export citation
Singular non-selfadjoint differential operators
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 825-841
- Print publication:
- 1994
-
- Article
- Export citation
Existence of changing sign solutions for some semilinear problems with jumping nonlinearities at zero
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1165-1176
- Print publication:
- 1994
-
- Article
- Export citation
Self-similar solutions for diffusion in semiconductors
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 473-506
- Print publication:
- 1994
-
- Article
- Export citation
Spectral properties of p-hyponormal operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 117-122
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
On the asphericity of one-relator relative presentations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 713-728
- Print publication:
- 1994
-
- Article
- Export citation
Projective modules of finite groups with elementary abelian Sylow 3-subgroups of order 9 in characteristic 3
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 161-168
- Print publication:
- 1994
-
- Article
- Export citation
Multiple solutions for nonhomogeneous elliptic equations involving critical Sobolev exponent*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1177-1191
- Print publication:
- 1994
-
- Article
- Export citation
Global branches of positive weak solutions of semilinear elliptic problems over nonsmooth domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 371-388
- Print publication:
- 1994
-
- Article
- Export citation
On the normal cores of certain subgroups of nilpotent groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 113-115
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Positive solutions for a class of nonpositone problems with concave nonlinearities
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 507-515
- Print publication:
- 1994
-
- Article
- Export citation
The Hausdorff dimension of systems of simultaneously small linear forms
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 367-374
- Print publication:
- December 1993
-
- Article
- Export citation
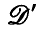 -valued stochastic differential equations
-valued stochastic differential equations
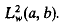 The domains of these operators are described in terms of boundary conditions involving the
The domains of these operators are described in terms of boundary conditions involving the 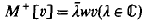 at both singular end-points
at both singular end-points 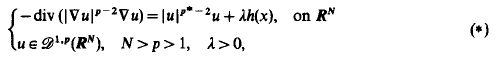
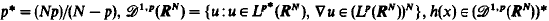 is continuous on
is continuous on 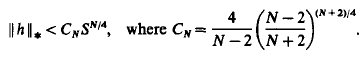
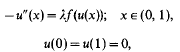
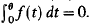 Assuming (fl)−(f6), Castro and Shivaji obtain some existence and nonexistence results and hence partial information on the bifurcation diagram, and they conjecture that this problem has at most two positive solutions. We prove this conjecture. Furthermore, we are able to generalise and improve their results under hypotheses (fl)−(f4). As a corollary, we show that there exists μ
Assuming (fl)−(f6), Castro and Shivaji obtain some existence and nonexistence results and hence partial information on the bifurcation diagram, and they conjecture that this problem has at most two positive solutions. We prove this conjecture. Furthermore, we are able to generalise and improve their results under hypotheses (fl)−(f4). As a corollary, we show that there exists μ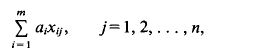

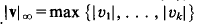 of any vector in
of any vector in 