Refine search
Actions for selected content:
25814 results in Abstract analysis
Index to Volume 31–40
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 383-391
- Print publication:
- December 1993
-
- Article
- Export citation
Pythagorean ratios in arithmetic progression, part i. three Pythagorean ratios
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 395-407
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Some characterizations of the hereditary pretorsion class of semigroup automata
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 327-337
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
On frattini-like subgroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, p. 408
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
GMJ volume 35 issue 3 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f8
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
On injectives in some varieties of Ockham algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 345-351
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Metacyclic p-groups and their conjugacy classes of subgroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 339-344
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
An identity for the Fibonacci and Lucas numbers
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 381-384
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
On congruences of double p-algebras with nonvoid core
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 385-394
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Some characterizations of semiprime Goldie rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 357-365
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Eta-products which are simultaneous eigenforms of Hecke operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 307-323
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Interpolation and inequalities for functions of exponential type: the Arens irregularity of an extremal algebra
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 325-326
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Isomorphisms between endomorphism rings of projective modules
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 353-355
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Units of group rings of groups of order 16
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 367-379
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Proper left type-A monoids revisited
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 293-306
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
GMJ volume 35 issue 3 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
Characterizations of Schützenberger graphs in terms of their automorphism groups and fundamental groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 275-291
- Print publication:
- September 1993
-
- Article
-
- You have access
- Export citation
87 - Will a Brownian motion return?
-
- Book:
- Exercises in Fourier Analysis
- Published online:
- 05 August 2012
- Print publication:
- 19 August 1993, pp 313-313
-
- Chapter
- Export citation
54 - Lord Kelvin
-
- Book:
- Exercises in Fourier Analysis
- Published online:
- 05 August 2012
- Print publication:
- 19 August 1993, pp 211-211
-
- Chapter
- Export citation
Preface
-
- Book:
- Exercises in Fourier Analysis
- Published online:
- 05 August 2012
- Print publication:
- 19 August 1993, pp ix-x
-
- Chapter
- Export citation
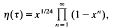

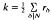 is an integer. Using the Legendre-Jacobi symbol (—), we define a Dirichlet character ∈ by
is an integer. Using the Legendre-Jacobi symbol (—), we define a Dirichlet character ∈ by
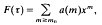
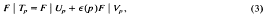
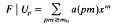

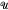 (Z
(Z