Refine search
Actions for selected content:
25814 results in Abstract analysis
Switched diffusion processes and systems of elliptic equations: a Dirichlet space approach
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 673-701
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
On a class of semilinear elliptic systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 609-620
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
A necessary and sufficient condition for nonattainment and formation of microstructure almost everywhere in scalar variational problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 437-471
- Print publication:
- 1994
-
- Article
- Export citation
The thermistor problem with conductivity vanishing for large temperature
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-21
- Print publication:
- 1994
-
- Article
- Export citation
Idempotent depth in semigroups of order-preserving mappings
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1045-1058
- Print publication:
- 1994
-
- Article
- Export citation
Point interactions on bounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 917-926
- Print publication:
- 1994
-
- Article
- Export citation
The interaction between bulk energy and surface energy in multiple integrals
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 737-756
- Print publication:
- 1994
-
- Article
- Export citation
A proof of characterisation of oscillation for higher-order neutral differential equations of mixed type by the Laplace transform
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 909-916
- Print publication:
- 1994
-
- Article
- Export citation
Convergence of the viscosity method for some nonlinear hyperbolic systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 341-352
- Print publication:
- 1994
-
- Article
- Export citation
Existence and multiplicity of homoclinic orbits for potentials on unbounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 317-339
- Print publication:
- 1994
-
- Article
- Export citation
Large-time behaviour of solutions of a reaction–diffusion equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 389-398
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 5 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
Approximation of Young measures by functions and application to a problem of optimal design for plates with variable thickness
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 399-422
- Print publication:
- 1994
-
- Article
- Export citation
Embeddings of nonorientable surfaces with totally reducible focal set
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 11-16
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Restrictions on microstructure
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 843-878
- Print publication:
- 1994
-
- Article
- Export citation
A remark on the resonance set for a semilinear elliptic equation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 803-809
- Print publication:
- 1994
-
- Article
- Export citation
Uniqueness of positive solutions for quasilinear elliptic equations when a parameter is large
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 189-198
- Print publication:
- 1994
-
- Article
- Export citation
Pythagorean ratios in arithmetic progression, part II. Four Pythagorean ratios
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 45-55
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
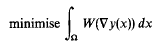
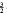 , <
, < 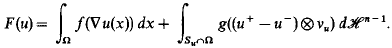
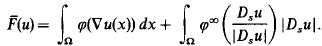
 in
in 
 with no rank-one connections, does it support a nontrivial Young measure limit of gradients? Our main results are these: (a) a Young measure can be supported on four incompatible matrices; (b) in two space dimensions, a Young measure cannot be supported on finitely many incompatible elastic wells; (c) in three or more space dimensions, a Young measure can be supported on three incompatible elastic wells; and (d) if
with no rank-one connections, does it support a nontrivial Young measure limit of gradients? Our main results are these: (a) a Young measure can be supported on four incompatible matrices; (b) in two space dimensions, a Young measure cannot be supported on finitely many incompatible elastic wells; (c) in three or more space dimensions, a Young measure can be supported on three incompatible elastic wells; and (d) if 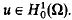 . We show that if λ
. We show that if λ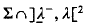 has measure zero, where
has measure zero, where 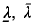 are the neighbouring eigenvalues of λ
are the neighbouring eigenvalues of λ