Refine search
Actions for selected content:
25814 results in Abstract analysis
On the analysis and control of hyperbolic systems associated with vibrating networks
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 77-104
- Print publication:
- 1994
-
- Article
- Export citation
Index to Volume 124
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1279-1282
- Print publication:
- 1994
-
- Article
- Export citation
On the absolutely continuous subspaces of Floquet operators
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 703-712
- Print publication:
- 1994
-
- Article
- Export citation
Generating functions and semi-classical orthogonal polynomials
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1003-1011
- Print publication:
- 1994
-
- Article
- Export citation
Shooting method for vortex solutions of a complex-valued Ginzburg–Landau equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1075-1088
- Print publication:
- 1994
-
- Article
- Export citation
On a family of one-relator pro-p-groups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1199-1207
- Print publication:
- 1994
-
- Article
- Export citation
Blow-up behaviour for nonlinearly perturbed semilinear parabolic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 947-969
- Print publication:
- 1994
-
- Article
- Export citation
PRM volume 124 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation
The travelling wave fronts of nonlinear reaction–diffusion systems via Friedlin's stochastic approaches
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 273-299
- Print publication:
- 1994
-
- Article
- Export citation
Linked eigenvalue problems for the p-Laplacian
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 5 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1023-1036
- Print publication:
- 1994
-
- Article
- Export citation
A Poincaré–Bendixson theorem for scalar balance laws
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 589-607
- Print publication:
- 1994
-
- Article
- Export citation
Cesàro averaging operators
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 1 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 121-126
- Print publication:
- 1994
-
- Article
- Export citation
GMJ volume 36 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Barrelled subspaces of spaces with subseries decompositions or Boolean rings of projections
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 1 / January 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-69
- Print publication:
- January 1994
-
- Article
-
- You have access
- Export citation
Anisotropic singular perturbations—the vectorial case
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 3 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 527-571
- Print publication:
- 1994
-
- Article
- Export citation
On the absolutely continuous spectrum of a vector-matrix Dirac system
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 253-262
- Print publication:
- 1994
-
- Article
- Export citation
Collocation methods for second-kind Volterra integral equations with weakly singular kernels
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 199-210
- Print publication:
- 1994
-
- Article
- Export citation
Decay of solutions of a higher order multidimensional nonlinear Korteweg–de Vries–Burgers system
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 263-271
- Print publication:
- 1994
-
- Article
- Export citation
Modelling the effective conductivity function of an arbitrary two–dimensional polycrystal using sequential laminates
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 4 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 757-783
- Print publication:
- 1994
-
- Article
- Export citation
Necessary and sufficient conditions for optimal controls in viscous flow problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 2 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 211-251
- Print publication:
- 1994
-
- Article
- Export citation
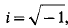 and
and 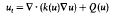
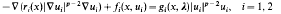
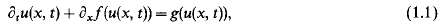
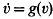 .
.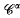 , Reα≧0, and consider the question of their boundedness on
, Reα≧0, and consider the question of their boundedness on