Refine search
Actions for selected content:
25814 results in Abstract analysis
Weakly stable Banach spaces and the Banach-Saks properties
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 79-83
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
On class numbers of a finite group and of its subgroups*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 295-301
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
PRM volume 123 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
A note on semiprime Malcev superalgebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 887-891
- Print publication:
- 1993
-
- Article
- Export citation
Asymptotic behaviour of finite energy solutions of polyharmonic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 345-354
- Print publication:
- 1993
-
- Article
- Export citation
Stable determination of a crack from boundary measurements
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 497-516
- Print publication:
- 1993
-
- Article
- Export citation
A reduction principle for topological classification of nonautonomous differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 621-632
- Print publication:
- 1993
-
- Article
- Export citation
Isoperimetric bounds for higher eigenvalue ratios for the n-dimensional fixed membrane problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 977-985
- Print publication:
- 1993
-
- Article
- Export citation
Normal-convex embeddings of inverse semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-121
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Linear equations in B(ℤ)*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1001-1009
- Print publication:
- 1993
-
- Article
- Export citation
Solution branches of a semilinear elliptic problem at corank-2 bifurcation points with Neumann boundary conditions*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 479-495
- Print publication:
- 1993
-
- Article
- Export citation
Solutions for the microsensor thermistor equations in the small bias case*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 987-999
- Print publication:
- 1993
-
- Article
- Export citation
A spectral radius problem connected with weak compactness
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-94
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
PRM volume 123 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
On homogeneous radicals of semigroup rings of commutative semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 951-957
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
Two representations of a conditioned superprocess
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 959-971
- Print publication:
- 1993
-
- Article
- Export citation
Symmetry sets of piecewise-circular curves
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1135-1149
- Print publication:
- 1993
-
- Article
- Export citation
Prime and semiprime semigroup rings of cancellative semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-12
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
 on the natural numbers we have
on the natural numbers we have
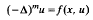
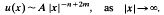
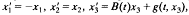 , where
, where 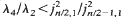 where λ
where λ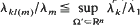 where
where