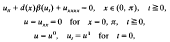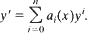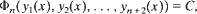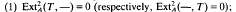Refine search
Actions for selected content:
25814 results in Abstract analysis
Exact controllability for a model of a multidimensional flexible structure
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 323-344
- Print publication:
- 1993
-
- Article
- Export citation
Strong asymptotic stability for a beam equation with weak damping
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 365-371
- Print publication:
- 1993
-
- Article
- Export citation
On an elliptic equation related to the blow-up phenomenon in the nonlinear Schrödinger equation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 763-782
- Print publication:
- 1993
-
- Article
- Export citation
Some interior and exterior boundary-value problems for the Helmholtz equation in a quadrant
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 275-294
- Print publication:
- 1993
-
- Article
- Export citation
On the commutativity of certain quasi-differential expressions II
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 27-43
- Print publication:
- 1993
-
- Article
- Export citation
On the relation between distinct particular solutions of equation

-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 917-926
- Print publication:
- 1993
-
- Article
- Export citation
Invariant ideals of commutative rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-134
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
The global Hölder-continuous solution of isentropic gas dynamics
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 231-238
- Print publication:
- 1993
-
- Article
- Export citation
Inequalities for non-decreasing sequences
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1017-1020
- Print publication:
- 1993
-
- Article
- Export citation
The Stefan problem: continuity of the interfaces for solutions with finite lapnumber
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-26
- Print publication:
- 1993
-
- Article
- Export citation
Remarks on the equilibrium shape of a Tokamak plasma
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1059-1070
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
Convergence in Lotka–Volterra-type delay systems without instantaneous feedbacks
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 45-58
- Print publication:
- 1993
-
- Article
- Export citation
Tilting modules and a theorem of Hoshino
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 69-77
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Generic hyperbolicity for scalar parabolic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1031-1040
- Print publication:
- 1993
-
- Article
- Export citation
Uniformly monotone dynamical systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 59-74
- Print publication:
- 1993
-
- Article
- Export citation
Weak lower semicontinuity of polyconvex integrals
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 681-691
- Print publication:
- 1993
-
- Article
- Export citation
Spectral properties of a two parameter nonlinear Sturm-Liouville problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1041-1058
- Print publication:
- 1993
-
- Article
- Export citation
One-relator products of torsion-free groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-104
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Semilinear elliptic problems with singular potentials in ℝN
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 593-619
- Print publication:
- 1993
-
- Article
- Export citation