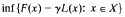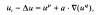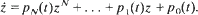Refine search
Actions for selected content:
25814 results in Abstract analysis
Limit analysis for a class of nonconvex problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 693-706
- Print publication:
- 1993
-
- Article
- Export citation
On the blow-up of solutions of a convective reaction diffusion equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 433-460
- Print publication:
- 1993
-
- Article
- Export citation
Rank one property for derivatives of functions with bounded variation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 239-274
- Print publication:
- 1993
-
- Article
- Export citation
Primitive near-rings do not form an axiomatisable class
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 399-400
- Print publication:
- 1993
-
- Article
- Export citation
Cohomological periodicity in graph products of combinatorially aspherical groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-129
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Global versus local admissibility criteria for dynamic phase boundaries
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 927-944
- Print publication:
- 1993
-
- Article
- Export citation
The Conley index for maps in absence of compactness
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 75-94
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
PRM volume 123 issue 6 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
The existence of principal eigenvalues for problems with indefinite weight function on ℝk
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 561-569
- Print publication:
- 1993
-
- Article
- Export citation
Maximum principles and comparison theorems for semilinear parabolic systems and their applications
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 857-885
- Print publication:
- 1993
-
- Article
- Export citation
On Frattini-like subgroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 95-98
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
GMJ volume 35 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
On the existence and nonexistence of global solutions of a diffusion-advection equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1099-1108
- Print publication:
- 1993
-
- Article
- Export citation
On the periodic Fučik spectrum and a superlinear Sturm–Liouville equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 95-107
- Print publication:
- 1993
-
- Article
- Export citation
Regularity of an elliptic problem with a singular nonlinearity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1021-1029
- Print publication:
- 1993
-
- Article
- Export citation
The congruence lattice of an ideal extension of semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-50
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
A geometric approach to the study of stationary free surface flows for viscous liquids
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 209-229
- Print publication:
- 1993
-
- Article
- Export citation
Periodic solutions of polynomial non-autonomous differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 783-801
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 5 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation