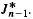Refine search
Actions for selected content:
25814 results in Abstract analysis
Hofer–Zehnder symplectic capacity for two-dimensional manifolds*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 945-950
- Print publication:
- 1993
-
- Article
- Export citation
First-order elliptic systems degenerated at the boundary
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1203-1212
- Print publication:
- 1993
-
- Article
- Export citation
On ternary quadratic forms that represent zero
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 13-23
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Growth sequences of 2-generator simple groups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 839-855
- Print publication:
- 1993
-
- Article
- Export citation
An inverse problem for the heat equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 973-976
- Print publication:
- 1993
-
- Article
- Export citation
General edge asymptotics of solutions of second-order elliptic boundary value problems I
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 109-155
- Print publication:
- 1993
-
- Article
- Export citation
A note on the characterisation of eigencurves for certain two parameter eigenvalue problems in ordinary differential equations
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-67
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Existence and finite dimensionality of the global attractor for a class of nonlinear dissipative equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 893-916
- Print publication:
- 1993
-
- Article
- Export citation
Foldings of star manifolds
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1011-1016
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
The distribution of genera among quadratic spaces over global fields
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 391-397
- Print publication:
- 1993
-
- Article
- Export citation
Solutions in Lebesgue spaces of the Navier-Stokes equations with dynamic boundary conditions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 745-761
- Print publication:
- 1993
-
- Article
- Export citation
General edge asymptotics of solutions of second-order elliptic boundary value problems II
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 157-184
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 6 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
The G-closure of two well-ordered, anisotropic conductors
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 423-432
- Print publication:
- 1993
-
- Article
- Export citation
Two-weight weak and extra-weak type inequalities for the one-sided maximal operator
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1109-1118
- Print publication:
- 1993
-
- Article
- Export citation
On the semigroups of partial one-to-one order-decreasing finite transformations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 355-363
- Print publication:
- 1993
-
- Article
- Export citation
Schrödinger-Poisson systems in dimension d ≦ 3: The whole-space case
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1179-1201
- Print publication:
- 1993
-
- Article
- Export citation
Boundary integral equations for the scattering of electromagnetic waves by a homogeneous dielectric obstacle
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 1 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 185-208
- Print publication:
- 1993
-
- Article
- Export citation
Hyperasymptotics and the Stokes' phenomenon
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 731-743
- Print publication:
- 1993
-
- Article
- Export citation
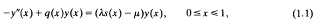

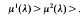
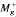 be the one-sided maximal operator and let Ф be a convex non-decreasing function on (0, ∞), Ф(0) = 0. We present necessary and sufficient conditions on a couple of weight functions (σ, ϱ) such that the integral inqualities of weak type
be the one-sided maximal operator and let Ф be a convex non-decreasing function on (0, ∞), Ф(0) = 0. We present necessary and sufficient conditions on a couple of weight functions (σ, ϱ) such that the integral inqualities of weak type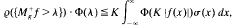

 = { α ∊ SI
= { α ∊ SI