Refine search
Actions for selected content:
25814 results in Abstract analysis
Steady states of the one-dimensional Cahn–Hilliard equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1071-1098
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
The theory of Legendrian unfoldings and first-order differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 517-532
- Print publication:
- 1993
-
- Article
- Export citation
Multiple transition layers in a singularly perturbed differential-delay equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1119-1134
- Print publication:
- 1993
-
- Article
- Export citation
Operators preserving orthogonality are isometries
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 835-837
- Print publication:
- 1993
-
- Article
- Export citation
Existence and uniqueness of travelling waves for a neural network
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 461-478
- Print publication:
- 1993
-
- Article
- Export citation
Subharmonics near an equilibrium for some second-order Hamiltonian systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 819-834
- Print publication:
- 1993
-
- Article
- Export citation
PRM volume 123 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation
Generalised factorisation for a class of Jones form matrix functions*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 401-422
- Print publication:
- 1993
-
- Article
- Export citation
GMJ volume 35 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Memory effect phenomena and Г-convergence
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 311-322
- Print publication:
- 1993
-
- Article
- Export citation
On the continuity of the polyconvex, quasiconvex and rank-oneconvex envelopes with respect to growth condition
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 4 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 707-729
- Print publication:
- 1993
-
- Article
- Export citation
Pairs of quadratic forms modulo one
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 51-61
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Hyperbolic phase change problems in heat conduction with memory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 3 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 571-592
- Print publication:
- 1993
-
- Article
- Export citation
Asymptotic behaviour of some reaction-diffusion systems modelling complex combustion on bounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1151-1163
- Print publication:
- 1993
-
- Article
- Export citation
On the initial growth of interfaces in reaction–diffusion equations with strong absorption
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 5 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 803-817
- Print publication:
- 1993
-
- Article
- Export citation
Index to Volume 123
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1213-1216
- Print publication:
- 1993
-
- Article
- Export citation
Left orders in strongly regular rings
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 2 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 303-310
- Print publication:
- 1993
-
- Article
- Export citation
Positive solutions of integrodifferential and difference equations with unbounded delay
-
- Journal:
- Glasgow Mathematical Journal / Volume 35 / Issue 1 / January 1993
- Published online by Cambridge University Press:
- 18 May 2009, pp. 105-113
- Print publication:
- January 1993
-
- Article
-
- You have access
- Export citation
Asymptotic expansions and Stokes multipliers of the confluent hypergeometric function Φ2, I
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 123 / Issue 6 / 1993
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1165-1177
- Print publication:
- 1993
-
- Article
- Export citation
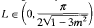 there is an
there is an  there is an
there is an 
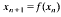
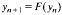
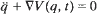
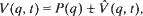
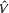 is of higher order near 0. In this paper the existence is shown of a sequence of subharmonic solutions of the equation above that converges to the equilibrium, such that their minimal periods converge to infinity.
is of higher order near 0. In this paper the existence is shown of a sequence of subharmonic solutions of the equation above that converges to the equilibrium, such that their minimal periods converge to infinity.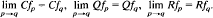 . This is the case for (
. This is the case for (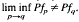 . In the last part of this work, we show that
. In the last part of this work, we show that 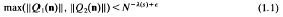
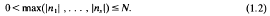
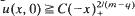 with
with 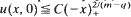 with C<C
with C<C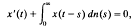
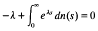
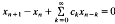 , where
, where 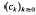 is a sequence of non-negative numbers. We prove this has positive solution if and only if the characteristic equation
is a sequence of non-negative numbers. We prove this has positive solution if and only if the characteristic equation 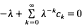 admits a root in (0, 1). For general results on integrodifferential equations we refer to the book by Burton [1] and the survey article by Corduneanu and Lakshmikantham [2]. Existence of a positive solution and oscillations in integrodifferential equations or in systems of integrodifferential equations recently have been investigated by Ladas, Philos and Sficas [5], Györi and Ladas [4], Philos and Sficas [12], Philos [9], [10], [11].
admits a root in (0, 1). For general results on integrodifferential equations we refer to the book by Burton [1] and the survey article by Corduneanu and Lakshmikantham [2]. Existence of a positive solution and oscillations in integrodifferential equations or in systems of integrodifferential equations recently have been investigated by Ladas, Philos and Sficas [5], Györi and Ladas [4], Philos and Sficas [12], Philos [9], [10], [11].