Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
n-Dimensional first integral and similarity solutions for two-phase flow
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 365-380
-
- Article
-
- You have access
- Export citation
ANZ volume 33 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Hyperelliptic parametrisation of the generalised order parameter of the N = 3 chiral Potts model
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 289-307
-
- Article
-
- You have access
- Export citation
On an exact WKB approach to Ablowitz-Segur's connection problem for the second Painlevé equation
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 111-119
-
- Article
-
- You have access
- Export citation
Spectral factorisation and prediction of multivariate processes with time-dependent rational spectral density matrices
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 192-210
-
- Article
-
- You have access
- Export citation
Contents of volume 47
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 593-595
-
- Article
-
- You have access
- Export citation
The effect of a submerged barrier on the natural freqencies and radiation damping of a shallow basin connected to open water
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 1 / July 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 104-128
-
- Article
-
- You have access
- Export citation
Generalized shear deformations for isotropic incompressible hyperelastic materials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 129-141
-
- Article
-
- You have access
- Export citation
Locating oscillatory orbits of the parametrically-excited pendulum
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 309-319
-
- Article
-
- You have access
- Export citation
The multiplicity of steady-state solutions arising from microwave heating. I. Infinite Biot number and small penetration depth
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 87-103
-
- Article
-
- You have access
- Export citation
On the uniqueness of solitary Rossby waves
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 4 / April 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 476-485
-
- Article
-
- You have access
- Export citation
Cooling of an infinite slab in a two-fluid medium
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 4 / April 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 474-485
-
- Article
-
- You have access
- Export citation
Natural cubic element formulation and infinite domain modelling for potential flow problems
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 133-143
-
- Article
-
- You have access
- Export citation
Optimal control in liver kinetics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 3 / January 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 361-369
-
- Article
-
- You have access
- Export citation
The fractional fourier transform and the wigner distribution
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 209-219
-
- Article
-
- You have access
- Export citation
Integral equation methods in inverse obstacle scattering
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 65-78
-
- Article
-
- You have access
- Export citation
A conjugate direction implementation of the BFGS algorithm with automatic scaling
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 122-134
-
- Article
-
- You have access
- Export citation
ANZ volume 32 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Foliations in supergravity
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 161-166
-
- Article
-
- You have access
- Export citation
A conditional gradient method for a class of time-lag optimal control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 518-537
-
- Article
-
- You have access
- Export citation
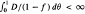 and
and 