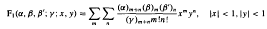Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
SEIR epidemic model with delay
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 119-134
-
- Article
-
- You have access
- Export citation
Large deviations and quasi-stationarity for density-dependent birth-death processes
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 238-256
-
- Article
-
- You have access
- Export citation
Reflection of water waves by a nearly vertical porous wall
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 417-429
-
- Article
-
- You have access
- Export citation
Oscillation of impulsive delay differential equations and applications to population dynamics
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 545-554
-
- Article
-
- You have access
- Export citation
On a boundary-value problem posed by cancer therapy with neutron beams
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 46-60
-
- Article
-
- You have access
- Export citation
Numerical study of Fisher's equation by a Petrov-Galerkin finite element method
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 1 / July 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 27-38
-
- Article
-
- You have access
- Export citation
On the Mellin transform of a product of hypergeometric functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 222-237
-
- Article
-
- You have access
- Export citation
Extrapolation techniques and the collocation method for a class of boundary integral equations
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 413-437
-
- Article
-
- You have access
- Export citation
ANZ volume 33 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On the crossing of intermediate unstable steady state solutions for thermal ignition in a sphere
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 77-85
-
- Article
-
- You have access
- Export citation
Contents of Volume 23
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 467-468
-
- Article
-
- You have access
- Export citation
Best difference equation approximation to Duffing's equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 349-356
-
- Article
-
- You have access
- Export citation
ANZ volume 40 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Multiple-term approximations for Appell's F1 function
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 135-148
-
- Article
-
- You have access
- Export citation
ANZ volume 44 issue 1 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Robustness with respect to small delays for exponential stability of abstract differential equations in Banach spaces
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 555-568
-
- Article
-
- You have access
- Export citation
ANZ volume 39 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Oscillations of delay differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 377-381
-
- Article
-
- You have access
- Export citation
Applications of the Lie theory of extended groups in Hamiltonian mechanics: the oscillator and the Kepler problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 2 / October 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 173-186
-
- Article
-
- You have access
- Export citation
Inequalities for the beta function of n variables
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 609-623
-
- Article
-
- You have access
- Export citation