Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
Rumours with general initial conditions
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 393-400
-
- Article
-
- You have access
- Export citation
Stability analysis of Runge–Kutta methods applied to a basic Volterra integral equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 515-538
-
- Article
-
- You have access
- Export citation
Analytic solution of the linearized shallow-water wave equations for certain continuous depth variations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 1 / June 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 81-94
-
- Article
-
- You have access
- Export citation
On wave motion in a two-layered liquid of infinite depth in the presence of surface and interfacial tension
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 3 / January 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 302-322
-
- Article
-
- You have access
- Export citation
Existence of stationary vacuum solutions of Einstein's equations in an exterior domain
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 231-247
-
- Article
-
- You have access
- Export citation
A quadrature method for constant-coefficient Cauchy singular integral equations on an interval
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 287-311
-
- Article
-
- You have access
- Export citation
ANZ volume 31 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 3 / January 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The stability of a curved, heated boundary layer: linear and nonlinear problems
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 507-543
-
- Article
-
- You have access
- Export citation
On the condition number of integral equations in linear elasticity using the modified Green's function
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 431-446
-
- Article
-
- You have access
- Export citation
The allometric hypothesis when the size variable is uncertain: issues in the study of carcass composition by serial slaughter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 477-488
-
- Article
-
- You have access
- Export citation
Global existence for the generalised 2D Ginzburg-Landau equation
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 381-392
-
- Article
-
- You have access
- Export citation
Bifurcation and stability of periodic solutions from a zero eigenvalue
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 2-20
-
- Article
-
- You have access
- Export citation
Inverse power law potentials about polygonal prisms and in polygonal cavities†
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 17 February 2009, p. 508
-
- Article
-
- You have access
- Export citation
A mathematical analysis of wind effects on a long-jumper
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 1 / July 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 65-76
-
- Article
-
- You have access
- Export citation
ANZ volume 25 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 1 / July 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
What is invexity?
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
ANZ volume 29 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 3 / January 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ANZ volume 37 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Simple nonlinear dual control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 131-144
-
- Article
-
- You have access
- Export citation
The propagation of small amplitude long waves on the surface of superfluid helium
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 3 / January 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 311-348
-
- Article
-
- You have access
- Export citation
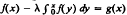 ; the simple form of this equation permits ready insight into features which are more obscure when considering (as elsewhere [1], [2], [6]) equations of a more complicated form. Due to the structure of the methods and the nature of the test equation, the stability analysis reduces to the study of recurrence relations of the form Ф
; the simple form of this equation permits ready insight into features which are more obscure when considering (as elsewhere [1], [2], [6]) equations of a more complicated form. Due to the structure of the methods and the nature of the test equation, the stability analysis reduces to the study of recurrence relations of the form Ф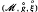 .
.



