Refine listing
Actions for selected content:
71 results in 14Axx
A fiber dimension theorem for essential and canonical dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 04 December 2012, pp. 148-174
- Print publication:
- January 2013
-
- Article
- Export citation
Nagata compactification for algebraic spaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 13 July 2012, pp. 747-814
- Print publication:
- October 2012
-
- Article
- Export citation
Descente fidèlement plate pour les n-champs d’Artin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 25 July 2011, pp. 1382-1412
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Base change for semiorthogonal decompositions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 852-876
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Quasi-invariants of complex reflection groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 965-1002
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Schemes over 𝔽1 and zeta functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 21 April 2010, pp. 1383-1415
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
Jet and prolongation spaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 24 February 2010, pp. 391-430
- Print publication:
- April 2010
-
- Article
- Export citation
The category of toric stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 718-746
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Perverse bundles and Calogero–Moser spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1403-1428
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Variation de la dimension relative en géométrie analytique p-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1511-1532
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
A sequence of multiple points on an algebraic variety which gives rise to a valuation ring
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-218
- Print publication:
- December 1971
-
- Article
- Export citation
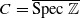 over 𝔽
over 𝔽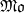 -schemes to interpret conceptually the spectral realization of zeros of
-schemes to interpret conceptually the spectral realization of zeros of 