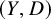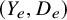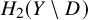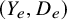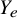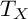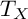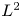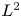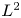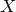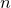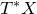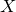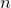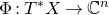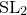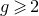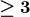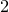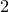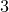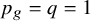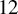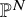Refine listing
Actions for selected content:
371 results in 14Jxx
A cone conjecture for log Calabi-Yau surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nef vector bundles on a quadric threefold with first Chern class two
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 526-565
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 ${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 237-283
- Print publication:
- June 2025
-
- Article
- Export citation
FANO FOURFOLDS WITH LARGE ANTICANONICAL BASE LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1021-1051
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On families of K3 surfaces with real multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NON-VANISHING RESULTS CONCERNING THE ANTI-CANONICAL BUNDLE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 201-218
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOW RANK SPECIALISATIONS OF ELLIPTIC SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 118-127
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIGNESS OF THE TANGENT BUNDLE OF A FANO THREEFOLD WITH PICARD NUMBER TWO
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 104-133
- Print publication:
- March 2025
-
- Article
- Export citation
Double EPW sextics associated with Gushel–Mukai surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
- Export citation
Torsion points and concurrent exceptional curves on del Pezzo surfaces of degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 634-652
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Family Floer mirror space for local SYZ singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e119
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A REMARK ON FUJINO’S WORK ON THE CANONICAL BUNDLE FORMULA VIA PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 79-92
- Print publication:
- March 2025
-
- Article
- Export citation
Vanishing theorem for tame harmonic bundles via L2-cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2828-2855
- Print publication:
- December 2024
-
- Article
- Export citation
Symmetric tensors on the intersection of two quadrics and Lagrangian fibration
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the properness of the moduli space of stable surfaces over
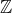 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quasimap invariants of moduli spaces of Higgs bundles
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KSB stability is automatic in codimension
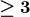 $\boldsymbol{\geq 3}$
$\boldsymbol{\geq 3}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periods of elliptic surfaces with
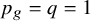 $p_g=q=1$
$p_g=q=1$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semistable degenerations of Calabi–Yau manifolds and mirror P=W conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation