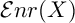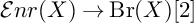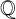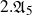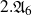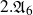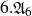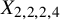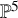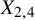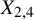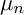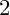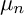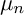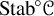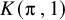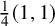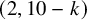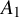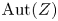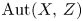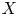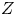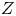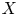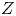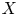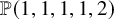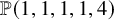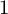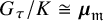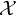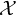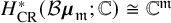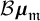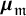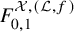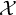Refine listing
Actions for selected content:
371 results in 14Jxx
ENRIQUES INVOLUTIONS AND BRAUER CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 606-621
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE FIBRES OF AN ELLIPTIC SURFACE WHERE THE RANK DOES NOT JUMP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 12 December 2022, pp. 276-282
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
Stability condition on Calabi–Yau threefold of complete intersection of quadratic and quartic hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 December 2022, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMIAMPLENESS FOR CALABI–YAU SURFACES IN POSITIVE AND MIXED CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 365-384
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTEGRAL POINTS ON SINGULAR DEL PEZZO SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 10 November 2022, pp. 1259-1294
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On canonical Fano intrinsic quadrics
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 07 November 2022, pp. 288-309
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iitaka fibrations for dlt pairs polarized by a nef and log big divisor
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 October 2022, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exceptional jumps of Picard ranks of reductions of K3 surfaces over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 September 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
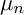 $\mu _{n}$-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
$\mu _{n}$-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 11-49
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic torsion for log-Enriques surfaces and Borcherds product
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On genus one mirror symmetry in higher dimensions and the BCOV conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMOOTHNESS IN PENCILS OF HYPERSURFACES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 85-94
- Print publication:
- February 2023
-
- Article
- Export citation
Deligne-Beilinson cohomology of the universal K3 surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 August 2022, e64
-
- Article
- Export citation
Strongly Jordan property and free actions of non-abelian free groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 736-746
-
- Article
- Export citation
Stability conditions on Calabi-Yau double/triple solids
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 August 2022, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RATIONALITY OVER NONCLOSED FIELDS OF FANO THREEFOLDS WITH HIGHER GEOMETRIC PICARD RANK
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 05 August 2022, pp. 207-247
- Print publication:
- January 2024
-
- Article
- Export citation
Open-closed Gromov-Witten invariants of 3-dimensional Calabi-Yau smooth toric DM stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 July 2022, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMALISED TANGENT BUNDLE, VARIETIES WITH SMALL CODEGREE AND PSEUDOEFFECTIVE THRESHOLD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 July 2022, pp. 149-206
- Print publication:
- January 2024
-
- Article
- Export citation