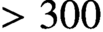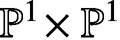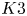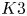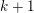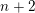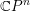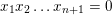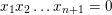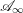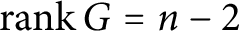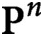Refine listing
Actions for selected content:
371 results in 14Jxx
Corrigendum: On an Enriques surface associated with a quartic Hessian surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 December 2020, pp. 603-605
- Print publication:
- April 2022
-
- Article
-
- You have access
- Export citation
Tropically constructed Lagrangians in mirror quintic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e58
-
- Article
-
- You have access
- Open access
- Export citation
ON THE SHARPNESS OF TIAN’S CRITERION FOR K-STABILITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 23 October 2020, pp. 41-73
- Print publication:
- March 2022
-
- Article
- Export citation
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
- Print publication:
- June 2021
-
- Article
- Export citation
K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 19 November 2020, pp. 1965-2019
- Print publication:
- October 2020
-
- Article
- Export citation
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 709-724
- Print publication:
- September 2021
-
- Article
- Export citation
Instanton sheaves and representations of quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 984-1004
-
- Article
- Export citation
Möbius automorphisms of surfaces with many circles
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 02 September 2020, pp. 42-71
- Print publication:
- February 2022
-
- Article
- Export citation
Constructing Fano 3-folds from cluster varieties of rank 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 09 November 2020, pp. 1873-1914
- Print publication:
- September 2020
-
- Article
- Export citation
Global geometry on moduli of local systems for surfaces with boundary
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1517-1559
- Print publication:
- August 2020
-
- Article
- Export citation
Degeneracy loci, virtual cycles and nested Hilbert schemes II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1623-1663
- Print publication:
- August 2020
-
- Article
- Export citation
Threefolds fibred by mirror sextic double planes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 24 June 2020, pp. 1305-1346
- Print publication:
- October 2021
-
- Article
- Export citation
Homological mirror symmetry for higher-dimensional pairs of pants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1310-1347
- Print publication:
- July 2020
-
- Article
- Export citation
Computing a categorical Gromov–Witten invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1275-1309
- Print publication:
- July 2020
-
- Article
- Export citation
NONHYPERELLIPTIC FIBRATIONS OF GENUS 4 WITH NONSURJECTIVE MULTIPLICATION MAP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 363-377
- Print publication:
- May 2021
-
- Article
- Export citation
The Nef Cone of the Hilbert Scheme of Points on Rational Elliptic Surfaces and the Cone Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 216-227
- Print publication:
- March 2021
-
- Article
- Export citation
Free abelian group actions on normal projective varieties: submaximal dynamical rank case
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1057-1073
- Print publication:
- August 2021
-
- Article
- Export citation
FANO HYPERSURFACES WITH ARBITRARILY LARGE DEGREES OF IRRATIONALITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 08 May 2020, e24
-
- Article
-
- You have access
- Open access
- Export citation
Rational lines on cubic hypersurfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 99-112
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
Bundles on
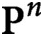 $\textbf{P}^n$ with vanishing lower cohomologies
$\textbf{P}^n$ with vanishing lower cohomologies
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 993-1012
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation