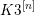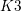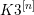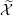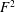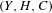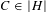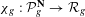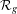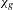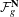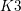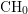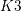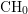Refine listing
Actions for selected content:
371 results in 14Jxx
THE LIPMAN–ZARISKI CONJECTURE IN GENUS ONE HIGHER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 23 April 2020, e21
-
- Article
-
- You have access
- Open access
- Export citation
HODGE IDEALS FOR
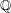 $\mathbb{Q}$-DIVISORS,
$\mathbb{Q}$-DIVISORS, 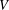 $V$-FILTRATION, AND MINIMAL EXPONENT
$V$-FILTRATION, AND MINIMAL EXPONENT
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 17 April 2020, e19
-
- Article
-
- You have access
- Open access
- Export citation
ON DEL PEZZO FIBRATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 30 March 2020, pp. 197-239
- Print publication:
- January 2022
-
- Article
- Export citation
Globally subanalytic CMC surfaces in ℝ3 with singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 407-424
- Print publication:
- February 2021
-
- Article
- Export citation
Two polarised K3 surfaces associated to the same cubic fourfold
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 51-64
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
NON-SYMPLECTIC INVOLUTIONS ON MANIFOLDS OF
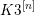 $K3^{[n]}$-TYPE
$K3^{[n]}$-TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 27 February 2020, pp. 278-302
- Print publication:
- September 2021
-
- Article
- Export citation
SNC Log Symplectic Structures on Fano Products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 February 2020, pp. 891-900
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
THE INTEGRAL HODGE CONJECTURE FOR 3-FOLDS OF KODAIRA DIMENSION ZERO
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 February 2020, pp. 1697-1717
- Print publication:
- September 2021
-
- Article
- Export citation
INVARIANCE OF CERTAIN PLURIGENERA FOR SURFACES IN MIXED CHARACTERISTICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 1-10
- Print publication:
- September 2021
-
- Article
- Export citation
Variation of Mixed Hodge Structures Associated to an Equisingular One-dimensional Family of Calabi-Yau Threefolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 441-464
- Print publication:
- April 2021
-
- Article
- Export citation
A Witt Nadel vanishing theorem for threefolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 435-475
- Print publication:
- March 2020
-
- Article
- Export citation
Quantum mirrors of log Calabi–Yau surfaces and higher-genus curve counting
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 07 January 2020, pp. 360-411
- Print publication:
- February 2020
-
- Article
- Export citation
Some remarks on the volume of log varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 314-322
-
- Article
- Export citation
On Homogeneous Polynomials Determined by their Partial Derivatives
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 06 December 2019, pp. 358-365
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
HALF NIKULIN SURFACES AND MODULI OF PRYM CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 29 November 2019, pp. 1547-1584
- Print publication:
- September 2021
-
- Article
- Export citation
ORBIFOLD ASPECTS OF CERTAIN OCCULT PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 137-156
- Print publication:
- September 2021
-
- Article
- Export citation
Derived categories of
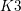 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 179-197
- Print publication:
- January 2020
-
- Article
- Export citation
ON TORUS ACTIONS OF HIGHER COMPLEXITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e38
-
- Article
-
- You have access
- Open access
- Export citation
(t, ℓ)-STABILITY AND COHERENT SYSTEMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 09 October 2019, pp. 661-672
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
ON THE MONODROMY AND GALOIS GROUP OF CONICS LYING ON HEISENBERG INVARIANT QUARTIC K3 SURFACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 640-660
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation