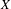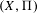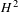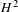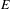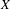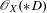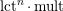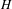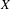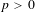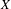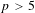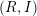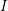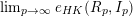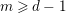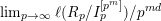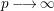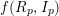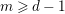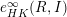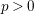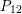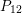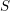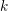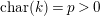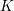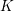Refine listing
Actions for selected content:
371 results in 14Jxx
A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 09 November 2018, pp. 1509-1519
- Print publication:
- September 2020
-
- Article
- Export citation
NO COHOMOLOGICALLY TRIVIAL NONTRIVIAL AUTOMORPHISM OF GENERALIZED KUMMER MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 110-122
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Super-rigid affine Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 17 October 2018, pp. 2462-2484
- Print publication:
- November 2018
-
- Article
- Export citation
Variation of the Variety of Minimal Rational Tangents of Cyclic Coverings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 115-123
-
- Article
- Export citation
Calabi–Yau Double Coverings of Fano–Enriques Threefolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 107-114
-
- Article
- Export citation
COMPARING THE BRAUER GROUP TO THE TATE–SHAFAREVICH GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 19 July 2018, pp. 965-970
- Print publication:
- May 2020
-
- Article
- Export citation
Finiteness theorems for K3 surfaces and abelian varieties of CM type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1571-1592
- Print publication:
- August 2018
-
- Article
- Export citation
BRILL–NOETHER THEOREMS AND GLOBALLY GENERATED VECTOR BUNDLES ON HIRZEBRUCH SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 05 July 2018, pp. 1-36
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Cremona transformations and derived equivalences of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 28 May 2018, pp. 1508-1533
- Print publication:
- July 2018
-
- Article
-
- You have access
- HTML
- Export citation
Derived categories of Gushel–Mukai varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 25 May 2018, pp. 1362-1406
- Print publication:
- July 2018
-
- Article
-
- You have access
- HTML
- Export citation
LOCAL VANISHING AND HODGE FILTRATION FOR RATIONAL SINGULARITIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 17 May 2018, pp. 801-819
- Print publication:
- May 2020
-
- Article
- Export citation
The volume of singular Kähler–Einstein Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1131-1158
- Print publication:
- June 2018
-
- Article
- Export citation
Twisted Alexander invariants of complex hypersurface complements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 1049-1073
- Print publication:
- October 2018
-
- Article
- Export citation
GENERAL HYPERPLANE SECTIONS OF THREEFOLDS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 12 April 2018, pp. 647-661
- Print publication:
- March 2020
-
- Article
- Export citation
Del Pezzo Surfaces in Weighted Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 545-572
-
- Article
-
- You have access
- Export citation
The Hodge diamond of O’Grady’s six-dimensional example
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 21 March 2018, pp. 984-1013
- Print publication:
- May 2018
-
- Article
- Export citation
TOWARD HILBERT–KUNZ DENSITY FUNCTIONSIN CHARACTERISTIC 0
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 08 March 2018, pp. 158-200
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
ENRIQUES’ CLASSIFICATION IN CHARACTERISTIC
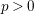 $p>0$: THE
$p>0$: THE 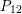 $P_{12}$-THEOREM
$P_{12}$-THEOREM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 27 February 2018, pp. 201-226
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
CANONICALLY FIBERED SURFACES OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2018, pp. 209-229
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Good reduction of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 18 September 2017, pp. 1-35
- Print publication:
- January 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation