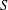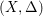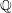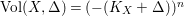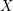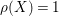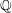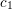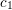Refine listing
Actions for selected content:
371 results in 14Jxx
THE EFFECTIVE CONE OF MODULI SPACES OF SHEAVES ON A SMOOTH QUADRIC SURFACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 151-215
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
Measures of irrationality for hypersurfaces of large degree
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 04 September 2017, pp. 2368-2393
- Print publication:
- November 2017
-
- Article
- Export citation
THE RATIONALITY OF THE MODULI SPACE OF ONE-POINTED INEFFECTIVE SPIN HYPERELLIPTIC CURVES VIA AN ALMOST DEL PEZZO THREEFOLD
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 06 June 2017, pp. 121-150
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
AT MOST 64 LINES ON SMOOTH QUARTIC SURFACES (CHARACTERISTIC 2)
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 31 May 2017, pp. 76-95
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
K-STABILITY OF FANO MANIFOLDS WITH NOT SMALL ALPHA INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 30 March 2017, pp. 519-530
- Print publication:
- May 2019
-
- Article
- Export citation
Lagrangian embeddings of cubic fourfolds containing a plane
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 23 March 2017, pp. 947-972
- Print publication:
- May 2017
-
- Article
- Export citation
SOME NEW EXAMPLES OF SMASH-NILPOTENT ALGEBRAIC CYCLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 623-634
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Elliptic singularities on log symplectic manifolds and Feigin–Odesskii Poisson brackets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 717-744
- Print publication:
- April 2017
-
- Article
- Export citation
The K3 category of a cubic fourfold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 586-620
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
The Craighero–Gattazzo surface is simply connected
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 28 February 2017, pp. 557-585
- Print publication:
- March 2017
-
- Article
- Export citation
THE LMMP FOR LOG CANONICAL 3-FOLDS IN CHARACTERISTIC
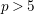 $p>5$
$p>5$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 20 February 2017, pp. 48-71
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Finiteness of fundamental groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 01 February 2017, pp. 257-273
- Print publication:
- February 2017
-
- Article
- Export citation
Divisorial Models of Normal Varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1053-1064
-
- Article
- Export citation
Examples of K-Unstable Fano Manifolds with the Picard Number 1
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 881-891
-
- Article
- Export citation
Differential Graded Quivers of Smooth Rational Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 859-876
-
- Article
- Export citation
RANK TWO STABLE ULRICH BUNDLES ON ANTICANONICALLY EMBEDDED SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 22-37
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
ELLIPTIC K3 SURFACES ASSOCIATED WITH THE PRODUCT OF TWO ELLIPTIC CURVES: MORDELL–WEIL LATTICES AND THEIR FIELDS OF DEFINITION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 09 November 2016, pp. 124-185
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
BOUNDING VOLUMES OF SINGULAR FANO THREEFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 17 October 2016, pp. 37-73
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
DYNAMICS ON SUPERSINGULAR K3 SURFACES AND AUTOMORPHISMS OF SALEM DEGREE 22
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-15
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
SEMISTABLE SHEAVES WITH SYMMETRIC
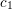 $c_{1}$ ON A QUADRIC SURFACE
$c_{1}$ ON A QUADRIC SURFACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 86-159
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
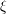
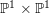
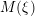
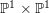
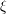
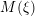
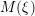
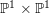
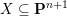

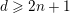
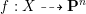
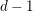
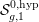
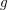
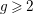
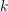
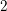
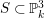
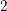

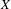

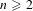
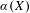
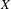
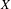
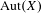
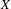
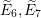
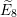
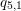
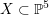
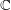
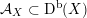
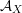
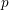
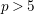
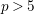
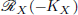 is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.
is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.