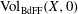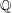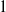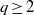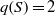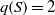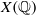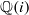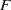Refine listing
Actions for selected content:
371 results in 14Jxx
On the volume of isolated singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 23 June 2014, pp. 1413-1424
- Print publication:
- August 2014
-
- Article
- Export citation
Finiteness of algebraic fundamental groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 409-414
- Print publication:
- March 2014
-
- Article
- Export citation
Derived categories and rationality ofconic bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1789-1817
- Print publication:
- November 2013
-
- Article
- Export citation
A vanishing theorem and symbolic powers of planar point ideals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
Moduli of products of stable varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 2036-2070
- Print publication:
- December 2013
-
- Article
- Export citation
Toric systems and mirror symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 28 August 2013, pp. 1839-1855
- Print publication:
- November 2013
-
- Article
- Export citation
Automorphisms of surfaces of general type with
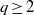 $q\geq 2$ acting trivially in cohomology
$q\geq 2$ acting trivially in cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1667-1684
- Print publication:
- October 2013
-
- Article
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
Rational points on singular intersections of quadrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1457-1494
- Print publication:
- September 2013
-
- Article
- Export citation
Depth of
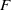 $F$-singularities and base change of relative canonical sheaves
$F$-singularities and base change of relative canonical sheaves
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 05 March 2013, pp. 43-63
- Print publication:
- January 2014
-
- Article
- Export citation
The Hodge ring of Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 637-657
- Print publication:
- April 2013
-
- Article
- Export citation
The standard conjectures for holomorphic symplectic varieties deformation equivalent to Hilbert schemes of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 481-494
- Print publication:
- March 2013
-
- Article
- Export citation
Algebraic boundaries of Hilbert’s SOS cones
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 15 October 2012, pp. 1717-1735
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Castelnuovo bounds for higher-dimensional varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 09 July 2012, pp. 1085-1132
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Fano 3-folds in codimension 4, Tom and Jerry. Part I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 14 May 2012, pp. 1171-1194
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
On the S-fundamental group scheme. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 April 2012, pp. 835-854
- Print publication:
- October 2012
-
- Article
- Export citation
ANALYTIC PROPERTIES OF MIRROR MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 195-235
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Kummer surfaces and the computation of the Picard group
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 84-100
-
- Article
-
- You have access
- Export citation
Non-normal abelian covers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 20 March 2012, pp. 1051-1084
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
A SHORT NOTE ON THE THOM–BOARDMAN SYMBOLS OF DIFFERENTIABLE MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 04 March 2012, pp. 385-390
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation