Refine listing
Actions for selected content:
371 results in 14Jxx
The resolution property of algebraic surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 209-226
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Strange duality of weighted homogeneous polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1413-1433
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Generalizations of Clausen's Formula and algebraic transformations of Calabi–Yau differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 273-295
-
- Article
-
- You have access
- Export citation
Exceptional sequences of invertible sheaves on rational surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1230-1280
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
On an automorphism of Hilb[2] of certain K3 surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 1-7
-
- Article
-
- You have access
- Export citation
Log canonical thresholds on Gorenstein canonical del Pezzo surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 187-219
-
- Article
-
- You have access
- Export citation
Geometrically rational real conic bundles and very transitive actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 September 2010, pp. 161-187
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
On Cox rings of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 964-998
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Characteristic foliation on a hypersurface of general type in a projective symplectic manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 497-506
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Moduli spaces of irreducible symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 404-434
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Explicit Kummer surface formulas for arbitrary characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 January 2010, pp. 47-64
-
- Article
-
- You have access
- Export citation
Polarized endomorphisms of uniruled varieties. With an appendix by Y. Fujimoto and N. Nakayama
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 21 December 2009, pp. 145-168
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Smoothable del Pezzo surfaces with quotient singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 15 December 2009, pp. 169-192
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Extension theorems for differential forms and Bogomolov–Sommese vanishing on log canonical varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 193-219
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On the deformation chirality of real cubic fourfolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 23 October 2009, pp. 1277-1304
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
On the equations for universal torsors over del Pezzo surfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 203-223
- Print publication:
- January 2010
-
- Article
- Export citation
Flops on holomorphic symplectic fourfolds and determinantal cubic hypersurfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 125-153
- Print publication:
- January 2010
-
- Article
- Export citation
Singularities on normal varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 393-414
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
The curve exclusion theorem for elliptic and K3 fibrations birational to Fano 3-fold hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 189-210
-
- Article
-
- You have access
- Export citation
Ricci iterations on Kähler classes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 743-768
- Print publication:
- October 2009
-
- Article
- Export citation
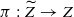 , we study the problem of extending the pull-back
, we study the problem of extending the pull-back 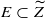 . For log canonical pairs and for certain values of
. For log canonical pairs and for certain values of 