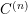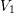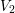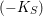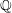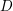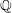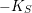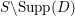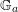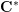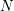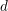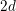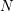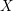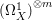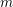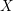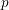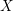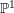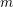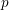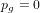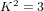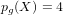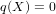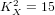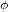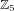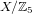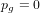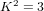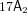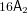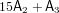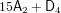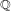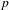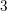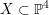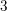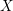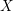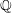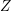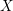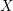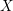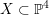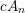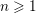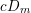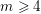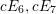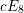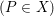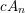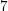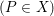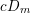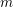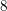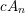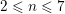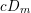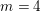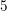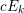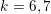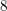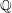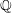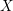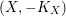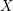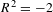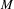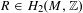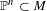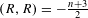Refine listing
Actions for selected content:
371 results in 14Jxx
Point counting on K3 surfaces and an application concerning real and complex multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 12-28
-
- Article
-
- You have access
- Export citation
A census of zeta functions of quartic K
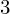 $3$ surfaces over
$3$ surfaces over 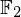 $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 1-11
-
- Article
-
- You have access
- Export citation
NOTES ON AUTOMORPHISMS OF SURFACES OF GENERAL TYPE WITH
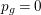 $p_{g}=0$ AND
$p_{g}=0$ AND 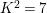 $K^{2}=7$
$K^{2}=7$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 66-86
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
ORBIT PARAMETRIZATIONS FOR K3 SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 07 July 2016, e18
-
- Article
-
- You have access
- Open access
- Export citation
On algebraic surfaces of general type with negative
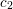 $c_{2}$
$c_{2}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 1966-1998
- Print publication:
- September 2016
-
- Article
- Export citation
Orbifold Zeta Functions for Dual Invertible Polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 May 2016, pp. 99-106
-
- Article
- Export citation
CHARACTERIZATION OF
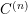 $C^{(n)}$
$C^{(n)}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 1-9
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
The isotriviality of smooth families of canonically polarized manifolds over a special quasi-projective base
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1421-1434
- Print publication:
- July 2016
-
- Article
- Export citation
Cylinders in singular del Pezzo surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 21 April 2016, pp. 1198-1224
- Print publication:
- June 2016
-
- Article
- Export citation
A finiteness theorem on symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1225-1236
- Print publication:
- June 2016
-
- Article
- Export citation
A Non-vanishing Theorem of Del Pezzo Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 463-472
-
- Article
- Export citation
Computing cup products in integral cohomology ofHilbert schemes of points on K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 78-97
-
- Article
-
- You have access
- Export citation
SINGULAR RATIONALLY CONNECTED THREEFOLDS WITH NON-ZERO PLURI-FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 3-32
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
Cuspidal quintics and surfaces with
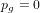 $p_{g}=0$ ,
$p_{g}=0$ , 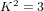 $K^{2}=3$ and 5-torsion
$K^{2}=3$ and 5-torsion
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 42-53
-
- Article
-
- You have access
- Export citation
A BOUND ON EMBEDDING DIMENSIONS OF GEOMETRIC GENERIC FIBERS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 20 January 2016, e3
-
- Article
-
- You have access
- Open access
- Export citation
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 13 January 2016, pp. 171-206
- Print publication:
- February 2018
-
- Article
- Export citation
Non-rigid quartic
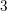 $3$-folds
$3$-folds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 955-983
- Print publication:
- May 2016
-
- Article
-
- You have access
- Open access
- Export citation
On Berman–Gibbs stability and K-stability of
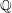 $\mathbb{Q}$-Fano varieties
$\mathbb{Q}$-Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 288-298
- Print publication:
- February 2016
-
- Article
- Export citation
A CLASSIFICATION OF LAGRANGIAN PLANES IN HOLOMORPHICSYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 09 September 2015, pp. 859-877
- Print publication:
- September 2017
-
- Article
- Export citation
Logarithmic abelian varieties, Part IV: Proper models
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 9-63
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
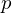
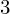
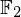
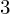
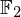
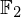
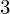
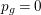
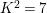
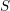
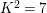
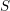
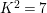
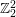
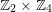
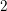
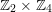
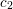

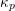
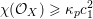
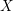
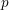

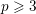
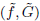 . Here we study the reduced orbifold zeta functions of dual pairs (
. Here we study the reduced orbifold zeta functions of dual pairs (