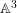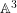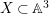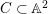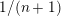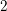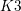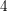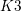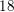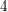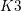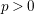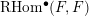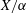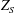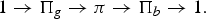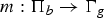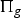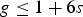Refine listing
Actions for selected content:
371 results in 14Jxx
JET SCHEMES OF QUASI-ORDINARY SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 20 September 2019, pp. 77-164
- Print publication:
- June 2021
-
- Article
- Export citation
THE CHERN–SCHWARTZ–MACPHERSON CLASS OF AN EMBEDDABLE SCHEME
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 18 September 2019, e30
-
- Article
-
- You have access
- Open access
- Export citation
TATE’S CONJECTURE AND THE TATE–SHAFAREVICH GROUP OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 17 September 2019, pp. 1001-1022
- Print publication:
- May 2021
-
- Article
- Export citation
On the Chow Ring of Cynk–Hulek Calabi–Yau Varieties and Schreieder Varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 03 September 2019, pp. 505-536
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
K-stability of birationally superrigid Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1845-1852
- Print publication:
- September 2019
-
- Article
- Export citation
Birational geometry of the moduli space of quartic
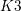 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1655-1710
- Print publication:
- September 2019
-
- Article
- Export citation
ON VARIETIES WITH TRIVIAL TANGENT BUNDLE IN CHARACTERISTIC
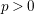 $p>0$
$p>0$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 26 June 2019, pp. 35-51
- Print publication:
- June 2021
-
- Article
- Export citation
ALGEBRAIC SURFACES WITH INFINITELY MANY TWISTOR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 May 2019, pp. 61-70
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
GEOMETRY OF INTEGRABLE LATTICE EQUATIONS AND THEIR REDUCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 168-169
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
The non-archimedean SYZ fibration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 953-972
- Print publication:
- May 2019
-
- Article
- Export citation
Autoequivalences of twisted K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 912-937
- Print publication:
- May 2019
-
- Article
- Export citation
Formality conjecture for K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 23 April 2019, pp. 902-911
- Print publication:
- May 2019
-
- Article
- Export citation
LINEAR SYSTEMS ON IRREGULAR VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 2087-2125
- Print publication:
- November 2020
-
- Article
- Export citation
Calabi–Yau Quotients of Hyperkähler Four-folds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 February 2019, pp. 45-92
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A Note on the Fundamental Group of Kodaira Fibrations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 739-746
-
- Article
- Export citation
LOCAL NEGATIVITY OF SURFACES WITH NON-NEGATIVE KODAIRA DIMENSION AND TRANSVERSAL CONFIGURATIONS OF CURVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2019, pp. 123-135
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
On an Enriques Surface Associated With a Quartic Hessian Surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 213-246
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
On Intrinsic Quadrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 145-181
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
On Algebraic Surfaces Associated with Line Arrangements
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 471-499
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On the Frequency of Algebraic Brauer Classes on Certain Log K3 Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 551-563
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation