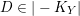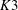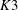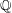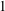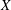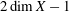Refine listing
Actions for selected content:
371 results in 14Jxx
Spherical functors on the Kummer surface
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-8
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A Feynman integral via higher normal functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2329-2375
- Print publication:
- December 2015
-
- Article
- Export citation
CLASSIFICATION OF POLARIZED SYMPLECTIC AUTOMORPHISMS OF FANO VARIETIES OF CUBIC FOURFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 17-37
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Algebraic Cycles on Quadric Sections of Cubics in ℙ4 under the Action of Symplectomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 14 July 2015, pp. 377-392
-
- Article
- Export citation
Mutations of Fake Weighted Projective Planes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 271-285
-
- Article
- Export citation
On Higher Rank Globally Generated Vector Bundles over a Smooth Quadric Threefold
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 311-337
-
- Article
- Export citation
A mirror theorem for toric stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1878-1912
- Print publication:
- October 2015
-
- Article
-
- You have access
- Open access
- Export citation
Quantum reconstruction for Fano bundles on projective space
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-28
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Log-canonical pairs and Gorenstein stable surfaces with
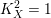 $K_{X}^{2}=1$
$K_{X}^{2}=1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 15 April 2015, pp. 1529-1542
- Print publication:
- August 2015
-
- Article
- Export citation
SOME MONODROMY GROUPS OF FINITE INDEX IN
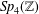 $\mathit{Sp}_{4}(\mathbb{Z})$
$\mathit{Sp}_{4}(\mathbb{Z})$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 48-62
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Log Canonical Thresholds of Complete Intersection Log Del Pezzo Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 20 February 2015, pp. 445-483
-
- Article
-
- You have access
- Export citation
Explicit birational geometry of 3-folds and 4-folds of general type, III
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 30 December 2014, pp. 1041-1082
- Print publication:
- June 2015
-
- Article
- Export citation
ADHM CONSTRUCTION OF PERVERSE INSTANTON SHEAVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 285-321
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
Frobenius categories, Gorenstein algebras and rational surface singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 502-534
- Print publication:
- March 2015
-
- Article
- Export citation
Equivariant Compactifications of Two-Dimensional Algebraic Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 149-168
-
- Article
-
- You have access
- Export citation
La conjecture de Tate entière pour les cubiques de dimension quatre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 16 October 2014, pp. 253-264
- Print publication:
- February 2015
-
- Article
- Export citation
Moduli of surfaces with an anti-canonical cycle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 265-291
- Print publication:
- February 2015
-
- Article
- Export citation
Explicit Kummer varieties of hyperelliptic Jacobian threefolds
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 496-508
-
- Article
-
- You have access
- Export citation
Examples of
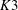 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 14-35
-
- Article
-
- You have access
- Export citation
Characterization of products of theta divisors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1384-1412
- Print publication:
- August 2014
-
- Article
- Export citation
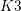
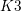
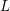
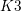
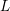
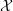
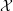
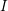
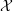
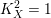
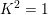
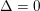
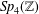
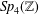
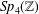
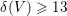
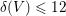
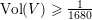
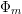
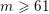
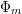
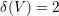
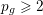
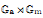 on ℙ
on ℙ