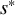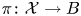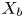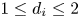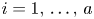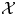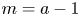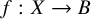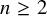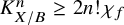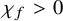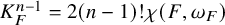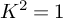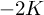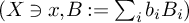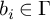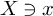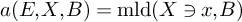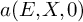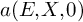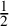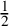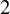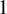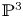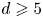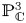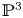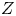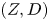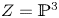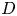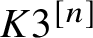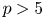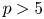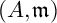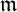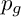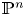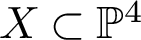Refine listing
Actions for selected content:
371 results in 14Jxx
Mirror symmetry and automorphisms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation
On birationally trivial families and adjoint quadrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 04 July 2022, pp. 587-617
-
- Article
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stability of Fano varieties via admissible flags
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 June 2022, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRIPLE COVERS OF K3 SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 939-979
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Severi inequality for fibrations of maximal Albanese dimension over curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 June 2022, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINED COUNT OF REAL RATIONAL CURVES OF CANONICAL DEGREE 2 ON REAL DEL PEZZO SURFACES WITH
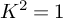 $K^2=1$
$K^2=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 14 June 2022, pp. 123-148
- Print publication:
- January 2024
-
- Article
- Export citation
Vertices of the Harder and Narasimhan polygons and the laws of large numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 340-357
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON BOUNDEDNESS OF DIVISORS COMPUTING MINIMAL LOG DISCREPANCIES FOR SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 2907-2930
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shokurov’s conjecture on conic bundles with canonical singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curves of maximal moduli on K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moduli of surfaces in
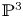 ${{\mathbb {P}}}^{3}$
${{\mathbb {P}}}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 1329-1374
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfect points on curves of genus 1 and consequences for supersingular K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1052-1083
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gromov–Witten theory and Noether–Lefschetz theory for holomorphic-symplectic varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 April 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kawamata–Viehweg vanishing theorem for log del Pezzo surfaces in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 750-763
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL HILBERT COEFFICIENTS AND ELLIPTIC IDEALS IN NORMAL TWO-DIMENSIONAL SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 779-800
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The integral Hodge conjecture for two-dimensional Calabi–Yau categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 12 April 2022, pp. 287-333
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schiffer variations and the generic Torelli theorem for hypersurfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 89-122
- Print publication:
- January 2022
-
- Article
- Export citation
CONICS IN SEXTIC
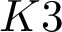 $K3$-SURFACES IN
$K3$-SURFACES IN  $\mathbb {P}^4$
$\mathbb {P}^4$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 273-304
- Print publication:
- June 2022
-
- Article
- Export citation