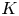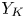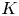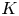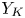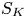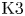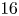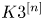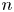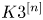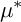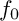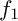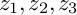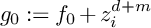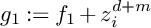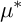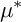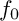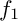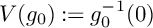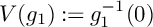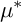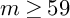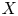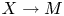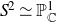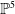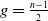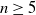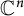Refine listing
Actions for selected content:
371 results in 14Jxx
Log Calabi–Yau surfaces and Jeffrey–Kirwan residues
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 547-592
- Print publication:
- May 2024
-
- Article
- Export citation
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
 $>3$
$>3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 694-723
- Print publication:
- September 2024
-
- Article
- Export citation
Minimal log discrepancies of hypersurface mirrors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 19 February 2024, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some examples of noncommutative projective Calabi–Yau schemes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 706-726
- Print publication:
- September 2024
-
- Article
- Export citation
Sixfolds of generalized Kummer type and K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 388-410
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 288-316
- Print publication:
- February 2024
-
- Article
- Export citation
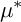 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 05 December 2023, pp. 488-497
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Finite orbits for large groups of automorphisms of projective surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 120-175
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compactifications of moduli of del Pezzo surfaces via line arrangement and K-stability
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2115-2135
- Print publication:
- December 2024
-
- Article
- Export citation
K-stability of birationally superrigid Fano 3-fold weighted hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 October 2023, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED AUTOMORPHIC SHEAVES AND THE PROPORTIONALITY PRINCIPLE OF HIRZEBRUCH-MUMFORD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 1567-1605
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-ISOMORPHIC SMOOTH COMPACTIFICATIONS OF THE MODULI SPACE OF CUBIC SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 03 October 2023, pp. 315-365
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived Category and ACM Bundles of Moduli Space of Vector Bundles on a Curve
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 September 2023, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
- Print publication:
- March 2024
-
- Article
- Export citation
Nonsolidity of uniruled varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 August 2023, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective varieties with nef tangent bundle in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1974-1999
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complex multiplication and Noether–Lefschetz loci of the twistor space of a K3 surface
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 17-38
- Print publication:
- January 2024
-
- Article
- Export citation
Geometric aspects on Humbert-Edge curves of type 5, Kummer surfaces and hyperelliptic curves of genus 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 612-624
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Łojasiewicz exponent of nondegenerate surface singularities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1391-1410
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation