Refine listing
Actions for selected content:
106 results in 16Dxx
On indecomposable decompositions of CS-modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 30-41
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Centralizer near-rings that are rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-183
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Classes of modules with many direct summands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-19
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
The structure of exponential Weyl algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 302-310
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
Commutative absolute subretracts
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 128-132
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
Preorders on canonical families of modules of finite length
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-77
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
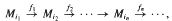 , with distinct
, with distinct 