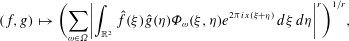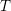Refine listing
Actions for selected content:
106 results in 16Dxx
On Annelidan, Distributive, and Bézout Rings
- Part of
- Chain conditions, growth conditions, and other forms of finiteness
- Radicals and radical properties of rings
- Rings and algebras arising under various constructions
- Modules, bimodules and ideals
- Local rings and generalizations
- Distributive lattices
- Conditions on elements
- Boolean algebras (Boolean rings)
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1082-1110
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
EPSILON-STRONGLY GROUPOID-GRADED RINGS, THE PICARD INVERSE CATEGORY AND COHOMOLOGY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 233-259
- Print publication:
- January 2020
-
- Article
-
- You have access
- Open access
- Export citation
ALGEBRAS OF GENERALIZED DIHEDRAL TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 181-236
- Print publication:
- December 2020
-
- Article
- Export citation
On a Theorem of Burgess and Stephenson
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 06 December 2018, pp. 603-605
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Characterizations and Direct Sums of Unit-Endoregular Modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 10 August 2018, pp. 1103-1112
-
- Article
- Export citation
THE
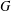 $G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES
$G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 289-315
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
PRIME SPECTRA OF AMBISKEW POLYNOMIAL RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 16 April 2018, pp. 49-68
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
On the Square Subgroup of a Mixed SI-Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 295-304
-
- Article
- Export citation
Integrable Derivations and Stable Equivalences of Morita Type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 343-362
-
- Article
- Export citation
GRADED CHAIN CONDITIONS AND LEAVITT PATH ALGEBRAS OF NO-EXIT GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 December 2017, pp. 229-256
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
HIGHER RANDOMNESS AND GENERICITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 December 2017, e31
-
- Article
-
- You have access
- Open access
- Export citation
DING-GRADED MODULES AND GORENSTEIN GR-FLAT MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 339-360
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
LATTICE STRUCTURE OF TORSION CLASSES FOR HEREDITARY ARTIN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 05 June 2017, pp. 89-100
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
SUBSETS OF VERTICES GIVE MORITA EQUIVALENCES OF LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 30 March 2017, pp. 212-222
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
PURE-INJECTIVITY FROM A DIFFERENT PERSPECTIVE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 14 March 2017, pp. 135-151
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
Rings of Polynomials With Artinian Coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 947-954
-
- Article
- Export citation
A BILINEAR RUBIO DE FRANCIA INEQUALITY FOR ARBITRARY SQUARES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 September 2016, e26
-
- Article
-
- You have access
- Open access
- Export citation
NEARLY MORITA EQUIVALENCES AND RIGID OBJECTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 19 August 2016, pp. 64-99
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
HOMOTOPY THEORY OF MODULES AND ADAMS COCOMPLETION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 525-532
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Rings Characterized via a Class of Left Exact Preradicals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 641-653
-
- Article
- Export citation
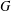
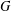
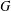
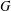
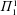
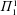
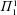
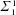
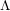
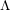
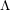
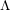
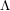
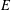
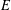
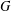
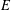
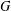
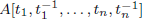 with coefficients in an Artinian ring
with coefficients in an Artinian ring