Refine listing
Actions for selected content:
106 results in 16Dxx
DIRECT SUMS OF INFINITELY MANY KERNELS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 23 November 2010, pp. 199-214
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
MODULES WITH ABELIAN ENDOMORPHISM RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 18 June 2010, pp. 99-112
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
ON COHERENCE OF ENDOMORPHISM RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 186-194
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
ON COMMUTATIVE REDUCED FILIAL RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 21 October 2009, pp. 310-316
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Combinatorial Gelfand models for some semigroups and q-rook monoid algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 707-718
-
- Article
-
- You have access
- Export citation
ON 𝒯-NONCOSINGULAR MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 462-471
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
STRONGLY GORENSTEIN FLAT MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 323-338
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
CORETRACTABLE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 289-304
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Semiclassical limits of quantum affine spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 387-407
-
- Article
-
- You have access
- Export citation
Morita equivalences and KK-theory for Banach algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 565-593
- Print publication:
- July 2009
-
- Article
- Export citation
ON A DUALITY THEOREM OF WAKAMATSU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 343-350
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Acyclic Calabi–Yau categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1332-1348
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Cotorsion modules and relative pure-injectivity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-244
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Characterizing rings by a direct decomposition property of their modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 359-366
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
On semiprime segments of rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-272
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
A General Approach to the Fitting Lemma
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 155-160
- Print publication:
- December 2005
-
- Article
- Export citation
Modules which are invariant under monomorphisms of their injective hulls
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-360
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Goldie dimensions of quotient modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-19
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Essential ideals of incidence algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 252-260
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
The singular ideal and radicals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 195-209
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
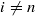 (where
(where 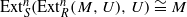 and
and 