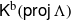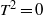Refine listing
Actions for selected content:
106 results in 16Dxx
Pure Injective and Absolutely Pure Sheaves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 623-640
-
- Article
- Export citation
THE IWASAWA MAIN CONJECTURE FOR HILBERT MODULAR FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 02 October 2015, e18
-
- Article
-
- You have access
- Open access
- Export citation
STABLE PROPERTIES OF HYPERRELEXIVITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 205-218
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
On Semi-Primary Self-Injective Rings and Faith's Quasi-Frobenius Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 219-229
-
- Article
-
- You have access
- Export citation
ON SI-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 92-103
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
(STRONGLY) GORENSTEIN FLAT MODULES OVER GROUP RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 17 December 2013, pp. 57-64
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
 $\tau $-tilting theory
$\tau $-tilting theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 03 December 2013, pp. 415-452
- Print publication:
- March 2014
-
- Article
- Export citation
FINITE HIGHER COMMUTATORS IN ASSOCIATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 503-509
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
SYMMETRIC ALGEBRAS OVER RINGS AND FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 466-472
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
NEAT AND CONEAT SUBMODULES OF MODULES OVER COMMUTATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 343-352
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ACCESSIBLE SUBRINGS AND KUROSH’S CHAINS OF ASSOCIATIVE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 145-157
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
THE CLASSIFICATION OF COMMUTATIVE TORSION FILIAL RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 289-296
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
STABLE RANK OF LEAVITT PATH ALGEBRAS OF ARBITRARY GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 206-217
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
On the abelianization of derived categories and a negative solution to Rosický’s problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 06 November 2012, pp. 125-147
- Print publication:
- January 2013
-
- Article
- Export citation
ON THE STABILISATION OF ONE-SIDED KUROSH’S CHAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 473-480
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
FINITELY GENERATED δ-SUPPLEMENTED MODULES ARE AMPLY δ-SUPPLEMENTED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 430-438
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
MODULES OVER QUANTUM LAURENT POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 19 March 2012, pp. 323-341
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
PARAMETRIZED STRICT DEFORMATION QUANTIZATION OF C*-BUNDLES AND HILBERT C*-MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 18 May 2011, pp. 25-38
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
REAL IDEALS IN POINTFREE RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 338-352
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
ON MAXIMAL ESSENTIAL EXTENSIONS OF RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 29 October 2010, pp. 329-337
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation


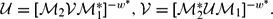
 algebras
algebras