Refine listing
Actions for selected content:
156 results in 13Dxx
TWO APPROACHES TO MÖBIUS INVERSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 August 2011, pp. 68-78
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ℤ[1/p]-motivic resolution of singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1434-1446
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
COFINITENESS OF GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 29 March 2011, pp. 382-388
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Green’s conjecture for curves on arbitrary K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 839-851
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Ideals of Herzog–Northcott type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 161-186
-
- Article
-
- You have access
- Export citation
COFINITENESS AND FINITENESS OF GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 23 July 2009, pp. 244-250
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
The Minimal Resolution Conjecture for Points on the Cubic Surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-49
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
ATTACHED PRIMES OF THE TOP GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 59-67
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Hochschild cohomology, the characteristic morphism and derived deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1557-1580
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Parameter-test-ideals of Cohen–Macaulay rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 933-948
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Deformation of finite morphisms and smoothing of ropes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 673-688
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
The Frobenius action on local cohomology modules in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1478-1492
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On the asymptotic behaviour of associated primes of generalized local cohomology modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-226
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
A generalization of the cofiniteness problem in local cohomology modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-324
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
d-sequences, local cohomology modules and generalized analytic independence
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-284
- Print publication:
- December 1986
-
- Article
- Export citation
Derived functors of the torsion functor and local cohomology of noncommutative rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-177
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation
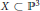
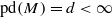 ,
, 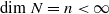 . First, we give the formula for the attached primes of the top generalized local cohomology module
. First, we give the formula for the attached primes of the top generalized local cohomology module 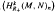 be the
be the 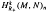 . In this paper we study the asymptotic behavior of Assf
. In this paper we study the asymptotic behavior of Assf 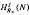 is not finitely generated.
is not finitely generated.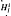 (
(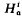 to denote, for
to denote, for 