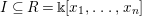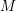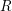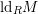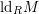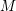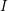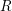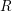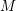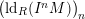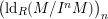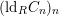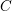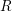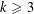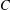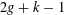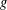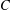Refine listing
Actions for selected content:
156 results in 13Dxx
Foundations of Boij–Söderberg theory for Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 11 September 2018, pp. 2205-2238
- Print publication:
- October 2018
-
- Article
- Export citation
Line arrangements and configurations of points with an unexpected geometric property
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 2150-2194
- Print publication:
- October 2018
-
- Article
- Export citation
LIFTINGS OF A MONOMIAL CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 05 July 2018, pp. 230-238
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
DETECTING KOSZULNESS AND RELATED HOMOLOGICAL PROPERTIES FROM THE ALGEBRA STRUCTURE OF KOSZUL HOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 18 June 2018, pp. 47-85
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
TOWARD HILBERT–KUNZ DENSITY FUNCTIONSIN CHARACTERISTIC 0
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 08 March 2018, pp. 158-200
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON THE ASSOCIATED PRIMES OF LOCAL COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 05 February 2018, pp. 1-9
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
ONE POSITIVE AND TWO NEGATIVE RESULTS FOR DERIVED CATEGORIES OF ALGEBRAIC STACKS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 22 January 2018, pp. 1087-1111
- Print publication:
- September 2019
-
- Article
- Export citation
Tangent cones to generalised theta divisors and generic injectivity of the theta map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2643-2657
- Print publication:
- December 2017
-
- Article
- Export citation
FROBENIUS ACTIONS ON LOCAL COHOMOLOGY MODULES AND DEFORMATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 07 September 2017, pp. 55-75
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE EFFECTIVE CONE OF MODULI SPACES OF SHEAVES ON A SMOOTH QUADRIC SURFACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 151-215
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE SHORT RESOLUTION OF A SEMIGROUP ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 400-411
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Perfect complexes on algebraic stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 2318-2367
- Print publication:
- November 2017
-
- Article
- Export citation
On the de Rham homology and cohomology of a complete local ring in equicharacteristic zero
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 2075-2146
- Print publication:
- October 2017
-
- Article
- Export citation
Tilting subcategories with respect to cotorsion triples in abelian categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 703-726
- Print publication:
- August 2017
-
- Article
- Export citation
LYUBEZNIK NUMBERS OF LOCAL RINGS AND LINEAR STRANDS OF GRADED IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 23-54
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE PROJECTIVE DIMENSION OF THE EDGE IDEAL OF A VERY WELL-COVERED GRAPH
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 160-179
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
RELATIVE HILBERT CO-EFFICIENTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 729-741
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
ON THE ASYMPTOTIC BEHAVIOR OF THE LINEARITY DEFECT
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 20 February 2017, pp. 35-47
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
The extremal secant conjecture for curves of arbitrary gonality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 347-357
- Print publication:
- February 2017
-
- Article
- Export citation
A LOWER BOUND FOR THE GONALITY CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 561-563
- Print publication:
- 2017
-
- Article
- Export citation
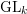
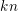
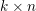
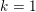
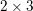

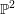
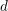
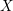
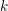
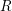
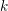
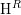
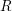
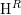
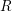
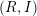
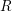
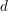
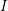
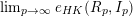
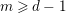
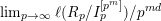
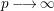
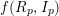
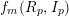
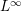
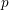
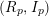
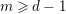
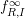
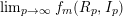
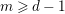
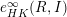
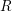
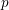
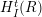
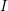
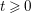
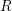
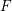
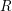
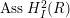
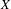
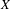
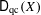
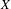
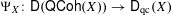
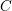

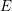

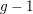
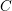
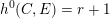
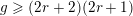
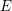

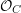
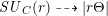
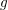
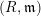
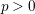
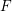
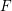
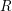
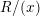
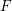
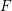
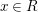
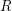
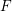
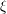
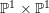
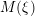
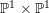
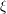
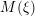
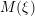
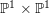
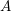
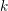
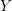
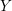
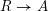
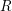
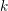
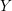
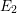
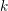
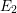
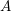
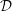
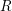
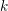
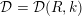
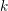
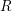
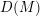
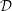
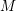
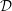
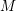
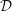
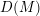
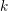
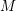
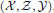 , the notion of
, the notion of 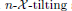 subcategories in an abelian category
subcategories in an abelian category 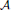 is introduced. It is proved that a virtually Gorenstein ring
is introduced. It is proved that a virtually Gorenstein ring 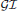 of Gorenstein injective
of Gorenstein injective 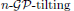 with respect to the cotorsion triple
with respect to the cotorsion triple 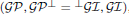 , where
, where 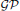 stands for the subcategory of Gorenstein projectives. In the case when a subcategory
stands for the subcategory of Gorenstein projectives. In the case when a subcategory 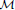 of
of 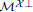 admits a right
admits a right  -coresolving covariantly finite and closed under direct summands.
-coresolving covariantly finite and closed under direct summands.