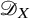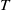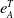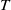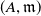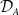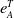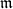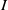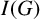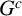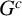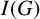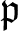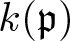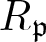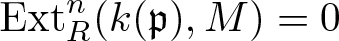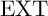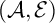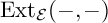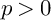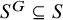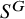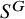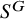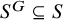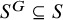Refine listing
Actions for selected content:
156 results in 13Dxx
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
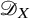 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 30 October 2024, pp. 86-106
- Print publication:
- January 2025
-
- Article
- Export citation
Derived functors and Hilbert polynomials over regular local rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1137-1147
-
- Article
- Export citation
Duality pairs, phantom maps, and definability in triangulated categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A short proof of the Hanlon-Hicks-Lazarev Theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilators and decompositions of singularity categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 23 April 2024, pp. 699-713
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBCOMPLEXES OF CERTAIN FREE RESOLUTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 886-904
- Print publication:
- December 2024
-
- Article
- Export citation
TILTING COMPLEXES AND CODIMENSION FUNCTIONS OVER COMMUTATIVE NOETHERIAN RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 618-693
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1013-1040
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING GEOMETRIC BRANCHES VIA THE FROBENIUS MAP AND F-NILPOTENT SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 724-741
- Print publication:
- September 2024
-
- Article
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 291-302
- Print publication:
- October 2024
-
- Article
- Export citation
FORMALLY REGULAR RINGS AND DESCENT OF REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 2279-2318
- Print publication:
- September 2024
-
- Article
- Export citation
Lim Ulrich sequences and Boij-Söderberg cones
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Persistence and the Sheaf-Function Correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of Ext and Tor via flat–cotorsion theory
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1142-1153
-
- Article
- Export citation
On the reducing projective dimension over local rings
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 104-118
- Print publication:
- January 2024
-
- Article
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
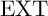 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A VARIANT OF PERFECTOID ABHYANKAR’S LEMMA AND ALMOST COHEN–MACAULAY ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 164-215
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
When are the natural embeddings of classical invariant rings pure?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poincaré complex diagonals and the Bass trace conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1819-1840
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation