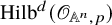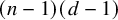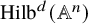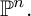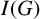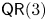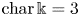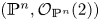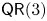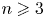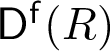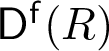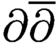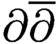Refine listing
Actions for selected content:
156 results in 13Dxx
Generalized tilting theory in functor categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 595-611
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small elementary components of Hilbert schemes of points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 June 2023, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Balmer spectrum of certain Deligne–Mumford stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1314-1346
- Print publication:
- June 2023
-
- Article
- Export citation
ANNIHILATORS AND DIMENSIONS OF THE SINGULARITY CATEGORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 533-548
- Print publication:
- June 2023
-
- Article
- Export citation
GENERIC LINES IN PROJECTIVE SPACE AND THE KOSZUL PROPERTY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 576-605
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on Hilbert–Kunz multiplicities and maximal F-signatures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 December 2022, pp. 247-271
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COSUPPORT FOR COMPACTLY GENERATED TRIANGULATED CATEGORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 13 December 2022, pp. 128-144
- Print publication:
- February 2024
-
- Article
- Export citation
REGULARITY OF POWERS OF BIPARTITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1-9
- Print publication:
- February 2023
-
- Article
- Export citation
Bökstedt periodicity and quotients of DVRs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1683-1712
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New examples of non-Fourier–Mukai functors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 1254-1267
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bi-graded Koszul modules, K3 carpets, and Green's conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 33-56
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Benson's cofibrants, Gorenstein projectives and a related conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 779-799
-
- Article
- Export citation
Rank 3 quadratic generators of Veronese embeddings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 2001-2025
- Print publication:
- September 2021
-
- Article
- Export citation
Counterexamples to Hochschild-Kostant-Rosenberg in characteristic p
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 June 2021, e49
-
- Article
-
- You have access
- Open access
- Export citation
CONSTRUCTING NONPROXY SMALL TEST MODULES FOR THE COMPLETE INTERSECTION PROPERTY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 21 June 2021, pp. 412-429
- Print publication:
- June 2022
-
- Article
- Export citation
POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD
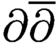 $\partial \overline {\partial }$-LEMMA
$\partial \overline {\partial }$-LEMMA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 305-354
- Print publication:
- June 2022
-
- Article
- Export citation
POWERS OF BINOMIAL EDGE IDEALS WITH QUADRATIC GRÖBNER BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 31 March 2021, pp. 233-255
- Print publication:
- June 2022
-
- Article
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
- Print publication:
- June 2021
-
- Article
- Export citation
ERRATUM: CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 23 October 2020, pp. 229-231
- Print publication:
- March 2022
-
- Article
- Export citation