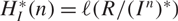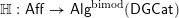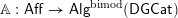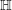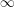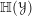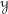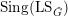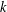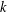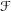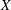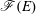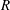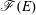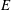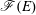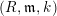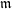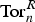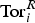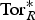Refine listing
Actions for selected content:
156 results in 13Dxx
DEGENERATING 0 IN TRIANGULATED CATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 158-167
- Print publication:
- December 2021
-
- Article
- Export citation
ISOMORPHISMS UP TO BOUNDED TORSION BETWEEN RELATIVE
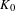 $K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS
$K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 1947-1968
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
POWERS OF THE MAXIMAL IDEAL AND VANISHING OF (CO)HOMOLOGY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 1-5
- Print publication:
- January 2021
-
- Article
-
- You have access
- Export citation
ON THE CONJECTURE OF VASCONCELOS FOR ARTINIAN ALMOST COMPLETE INTERSECTION MONOMIAL IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 10 December 2019, pp. 263-277
- Print publication:
- September 2021
-
- Article
- Export citation
EQUIVARIANT
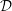 ${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 29 November 2019, pp. 61-82
- Print publication:
- September 2021
-
- Article
- Export citation
Residual intersections are Koszul–Fitting ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 23 September 2019, pp. 2150-2179
- Print publication:
- November 2019
-
- Article
- Export citation
INTEGRAL CLOSURE OF STRONGLY GOLOD IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 18 July 2019, pp. 204-216
- Print publication:
- March 2021
-
- Article
- Export citation
Tight closure of powers of ideals and tight hilbert polynomials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 335-355
- Print publication:
- September 2020
-
- Article
- Export citation
Sheaves of categories with local actions of Hochschild cochains
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1521-1567
- Print publication:
- August 2019
-
- Article
- Export citation
Notes on linkage of modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1045-1062
-
- Article
- Export citation
Linear syzygies, hyperbolic Coxeter groups and regularity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1076-1097
- Print publication:
- June 2019
-
- Article
- Export citation
On local stabilities of
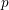 $p$-Kähler structures
$p$-Kähler structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 455-483
- Print publication:
- March 2019
-
- Article
- Export citation
On the Ideal Case of a Conjecture of Huneke and Wiegand
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 847-859
-
- Article
- Export citation
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
On triangle equivalences of stable categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 955-974
- Print publication:
- April 2020
-
- Article
- Export citation
On Deformations of Pairs (Manifold, Coherent Sheaf)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1209-1241
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On Special Fiber Rings of Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 225-242
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 27 December 2018, pp. 322-345
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Rigidity of Ext and Tor with Coefficients in Residue Fields of a Commutative Noetherian Ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 305-321
-
- Article
- Export citation
VANISHING OF (CO)HOMOLOGY OVER DEFORMATIONS OF COHEN-MACAULAY LOCAL RINGS OF MINIMAL MULTIPLICITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 12 October 2018, pp. 705-725
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
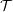
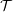
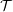
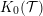
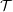
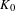
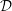
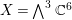
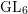
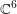
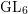
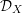
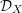
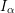
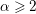
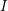
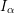
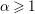
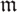 ) be an analytically unramified local ring of positive prime characteristic
) be an analytically unramified local ring of positive prime characteristic